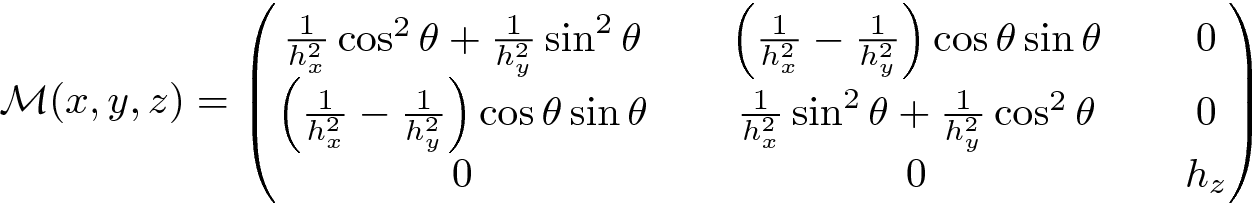Anisotropic Mesh Generation

Analytic Metric Functions

Linear metric

Metric given by where h_x =0.1, h_y=0.1, h₀ = 0.001, h_z = h₀ + 2(0.1-h₀)|z-0.6|

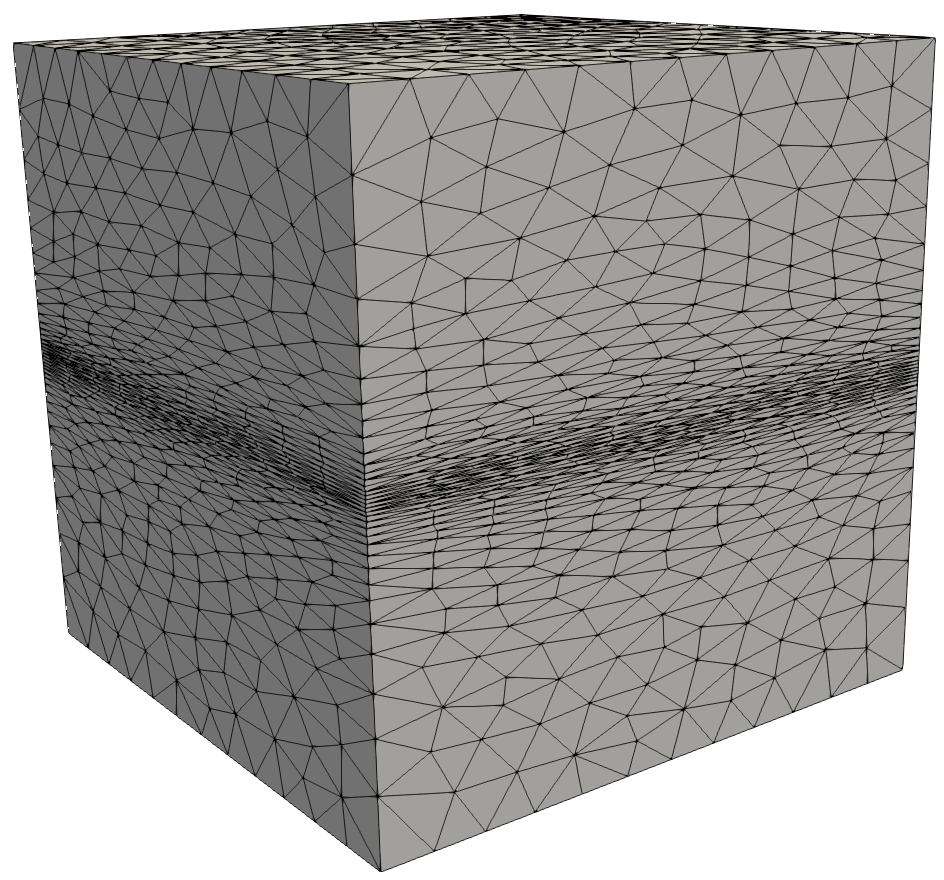
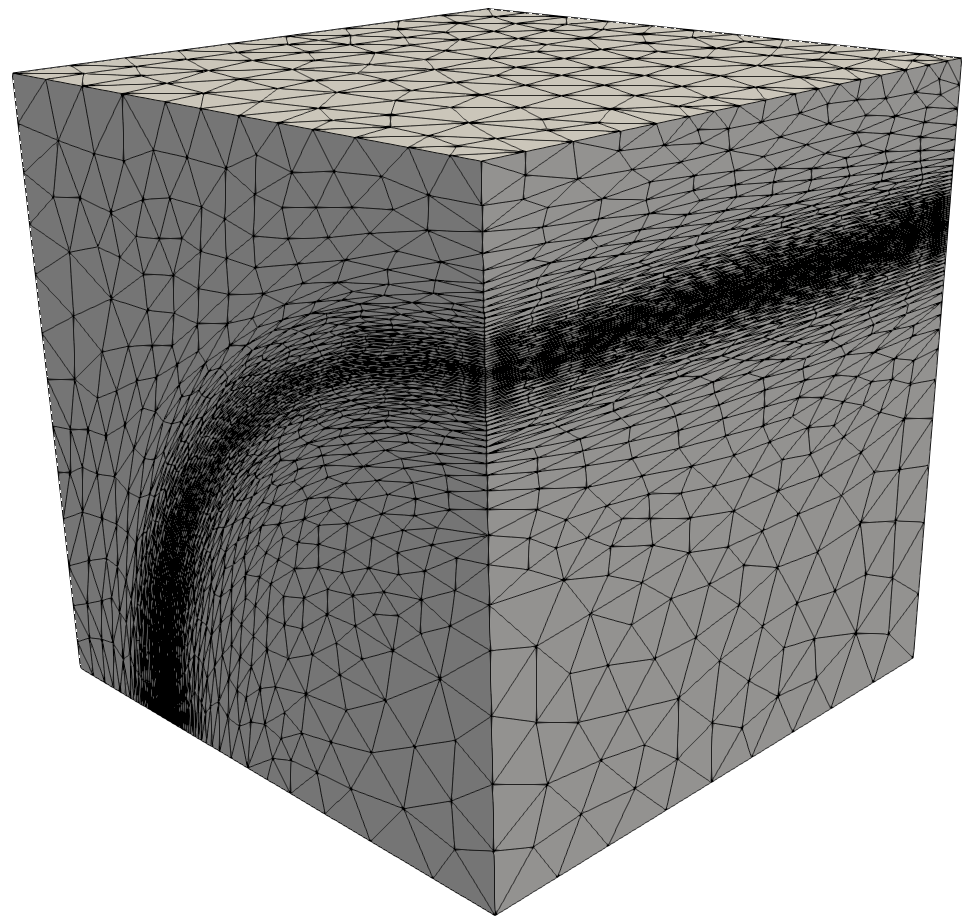
Surface Mesh, cross-cut and detail of the generated volume mesh.

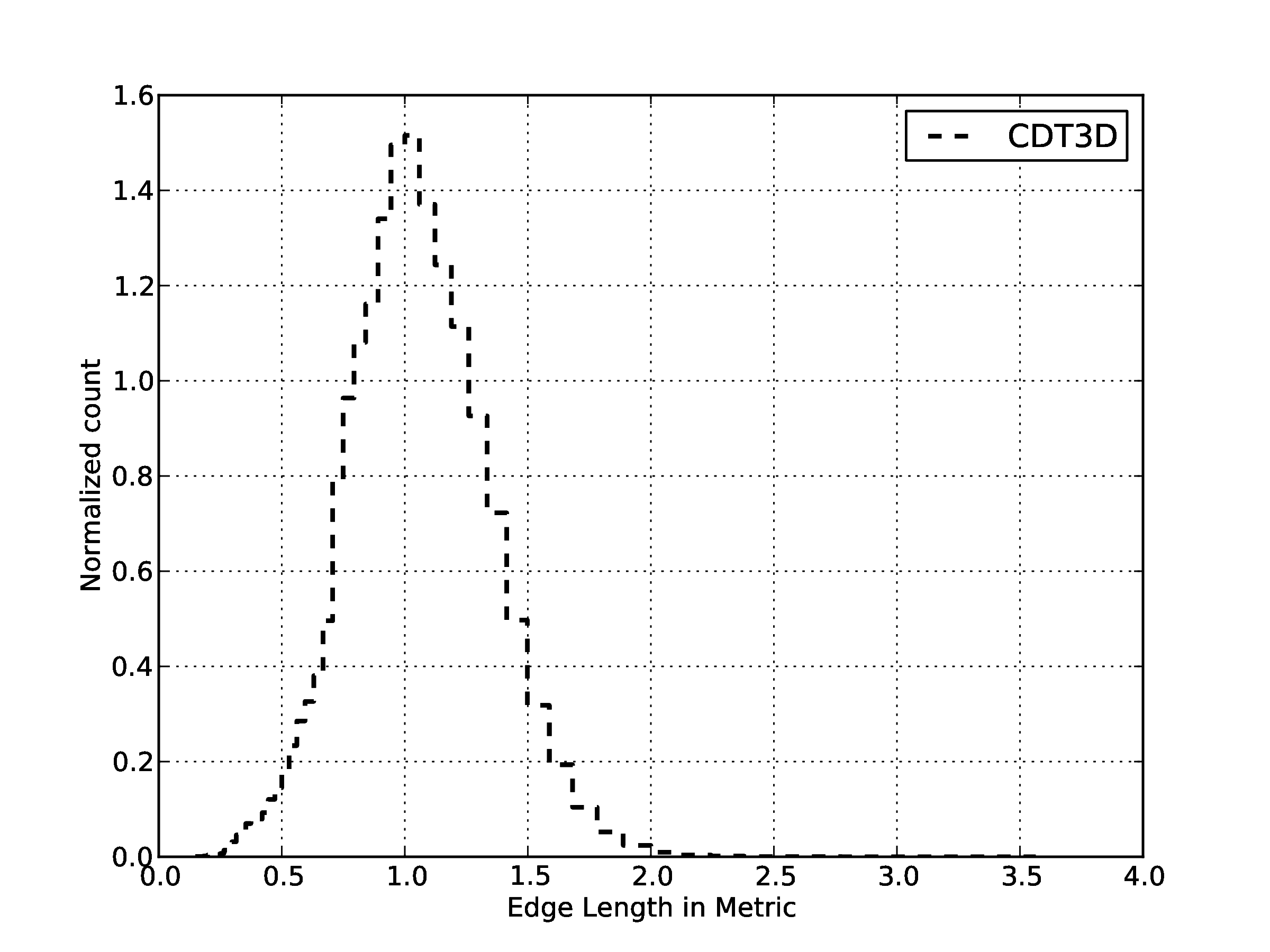
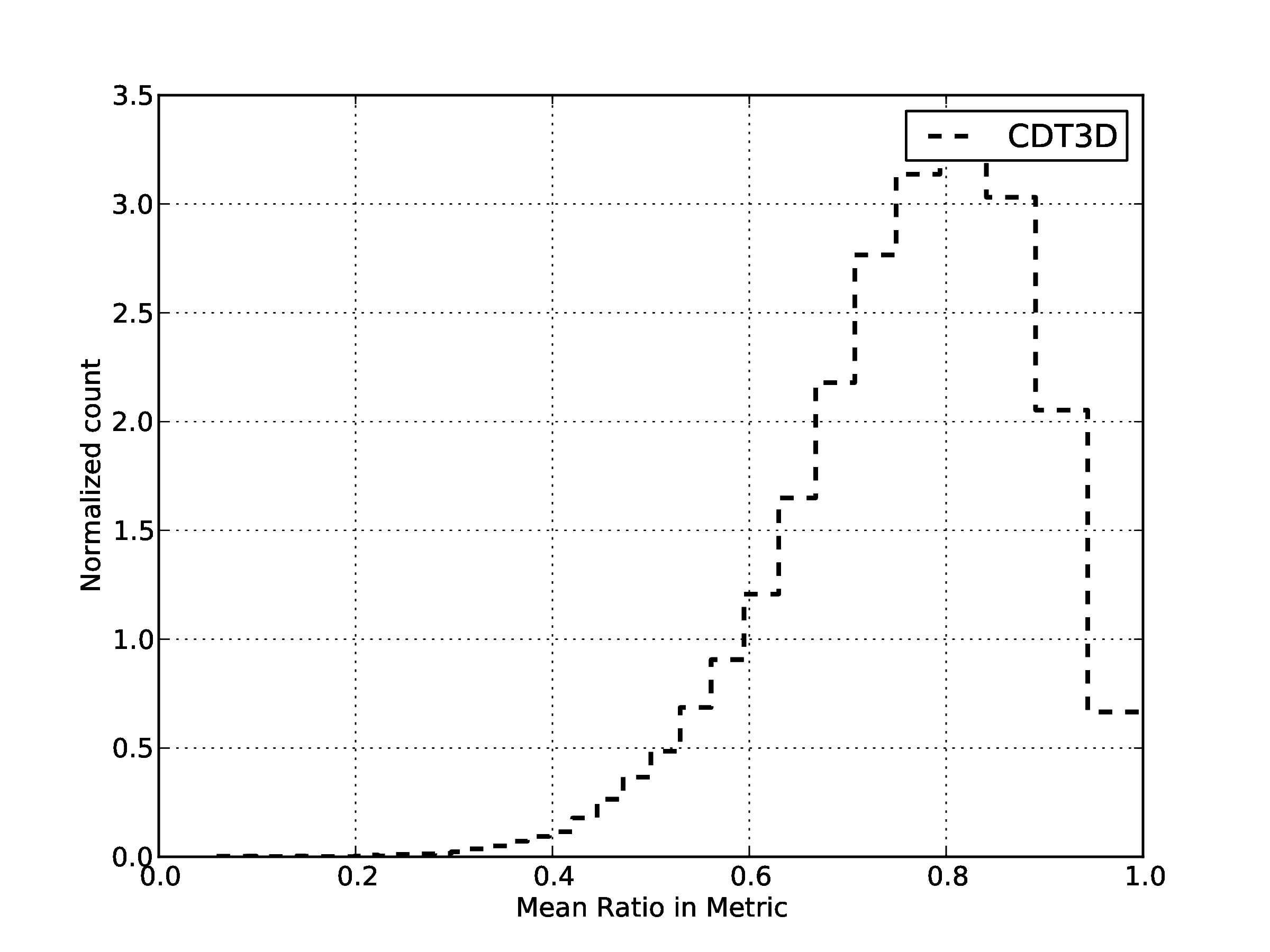
Quality statistics in the metric space for generated volume mesh.94 % of the edges has length between [0.5,1.5]. For the mean ratio 96%,of the elements have quality higher that 0.7.

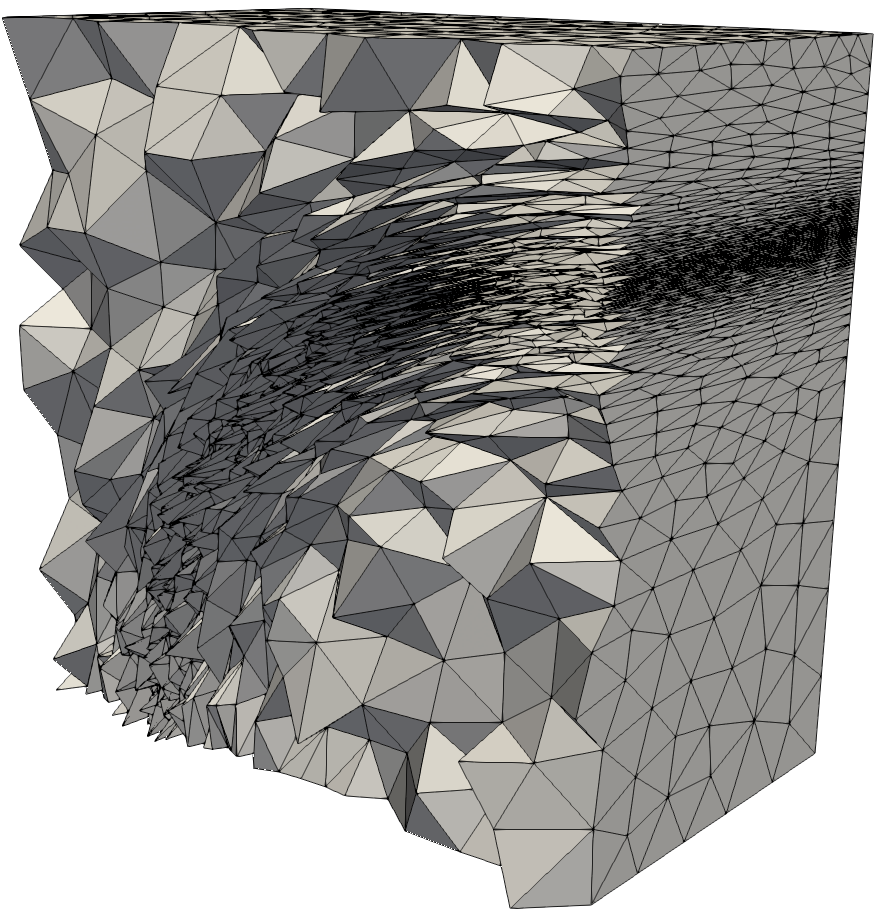
Quarter of a Cylinder

Metric given by

where h_x = min(0.002 5^a, h_max), h_y = min(0.05 · 2^a, h_max), h_z= h_max, h_max = 0.1, θ = arctan(x,y), a = 10 · | 0.75 - √ (x2+ y2)  |

Surface Mesh, cross-cut and detail of the generated volume mesh.

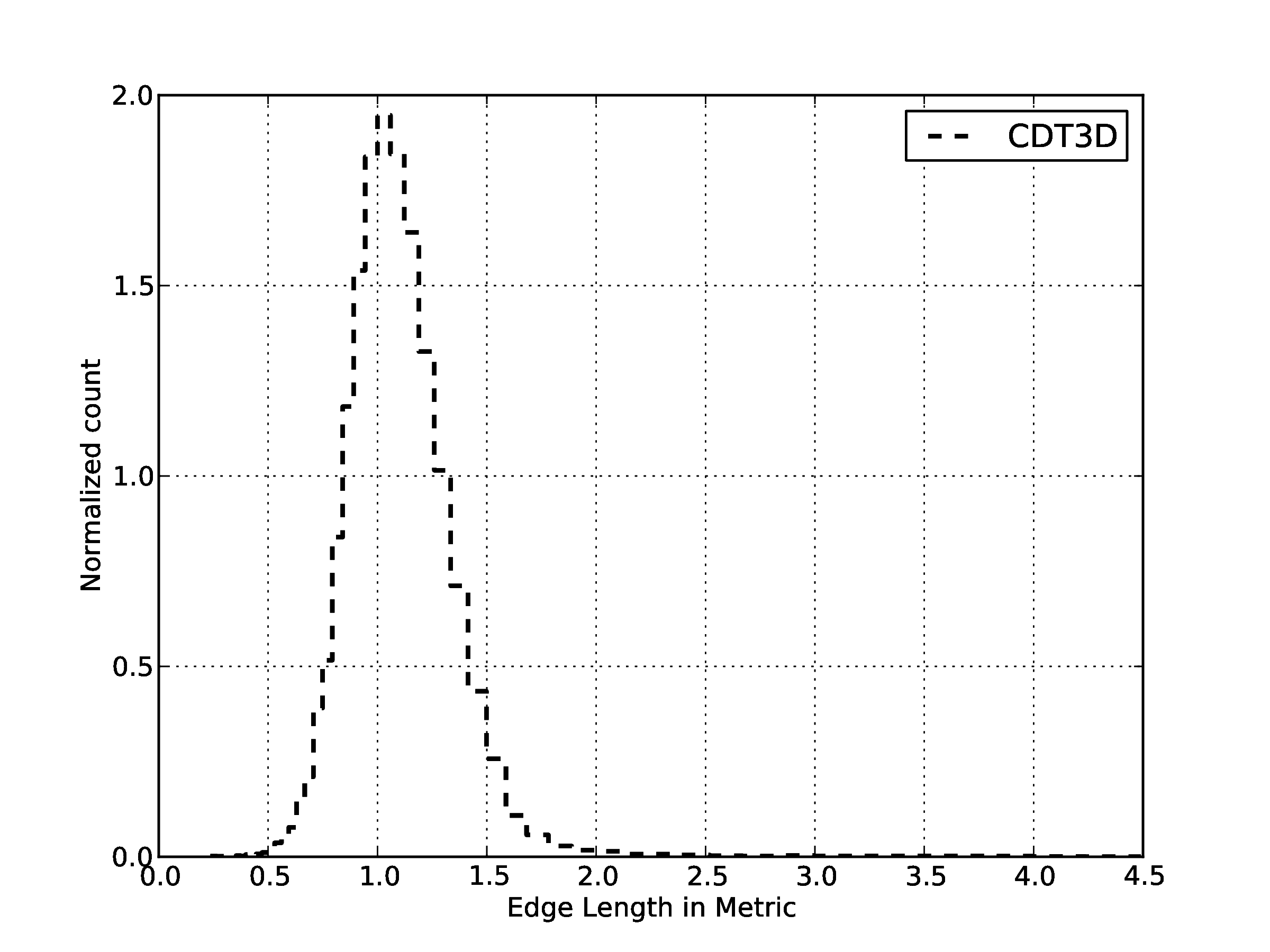
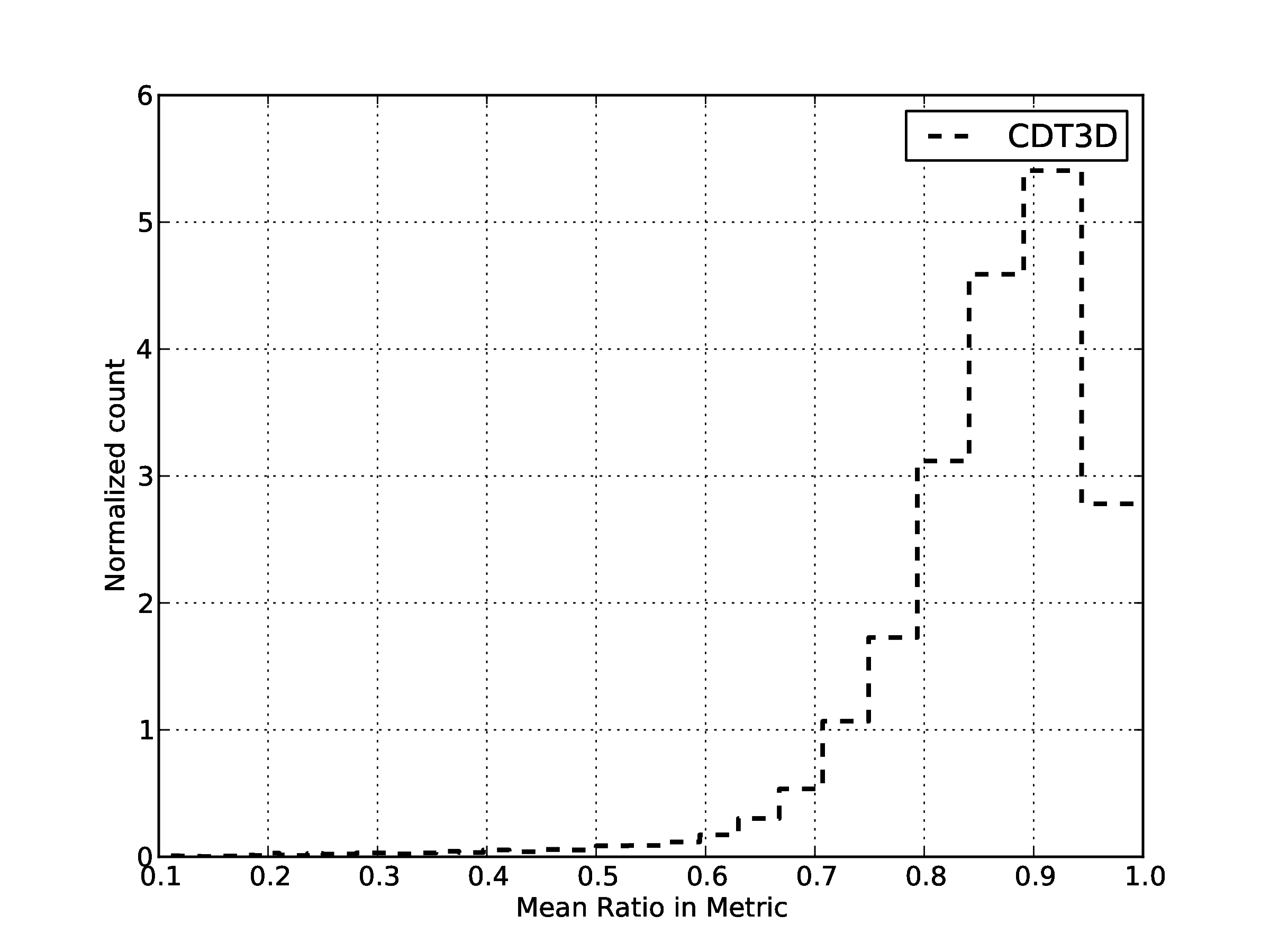
Quality statistics in the metric space for generated volume mesh. 91 % of the edges has length between [0.5,1.5]. For the mean ratio 79% of the elements have quality higher that 0.7.

Solution Based Adaptation

Onera M6

30K Complexity

Surface and background meshes were acquired from UGAWG repository

Initial surface mesh acquired from [1]	Refined surface mesh using as a 30K complexity background mesh acquired from [2]
cross cuts of the final mesh

The final mesh (available here ) was compared against the results from the 2018 Scitech paper Unstructured Grid Adaptation and Solver Technology for Turbulent Flows available at https://arc.aiaa.org/doi/abs/10.2514/6.2018-1103 .

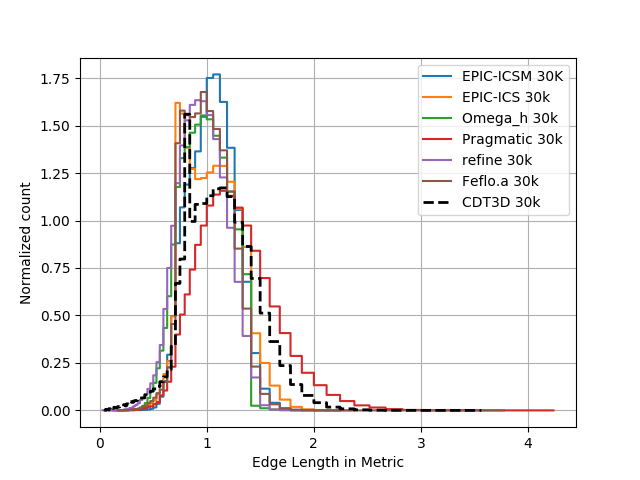
50K Complexity

Same input surface but with different metric complexity :

cross cuts of the final mesh

The background mesh is available here

The final mesh (available here )