Anisotropic Mesh Generation
Contents
Analytic Metric Functions
Linear metric
Metric given by 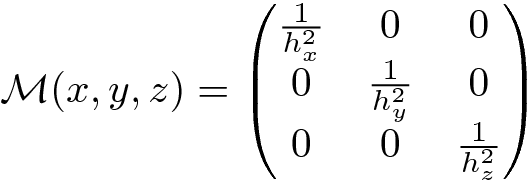 where hx =0.1, hy=0.1, h0 = 0.001, hz = h0 + 2(0.1-h0)|z-0.6|
where hx =0.1, hy=0.1, h0 = 0.001, hz = h0 + 2(0.1-h0)|z-0.6|
|

|

|
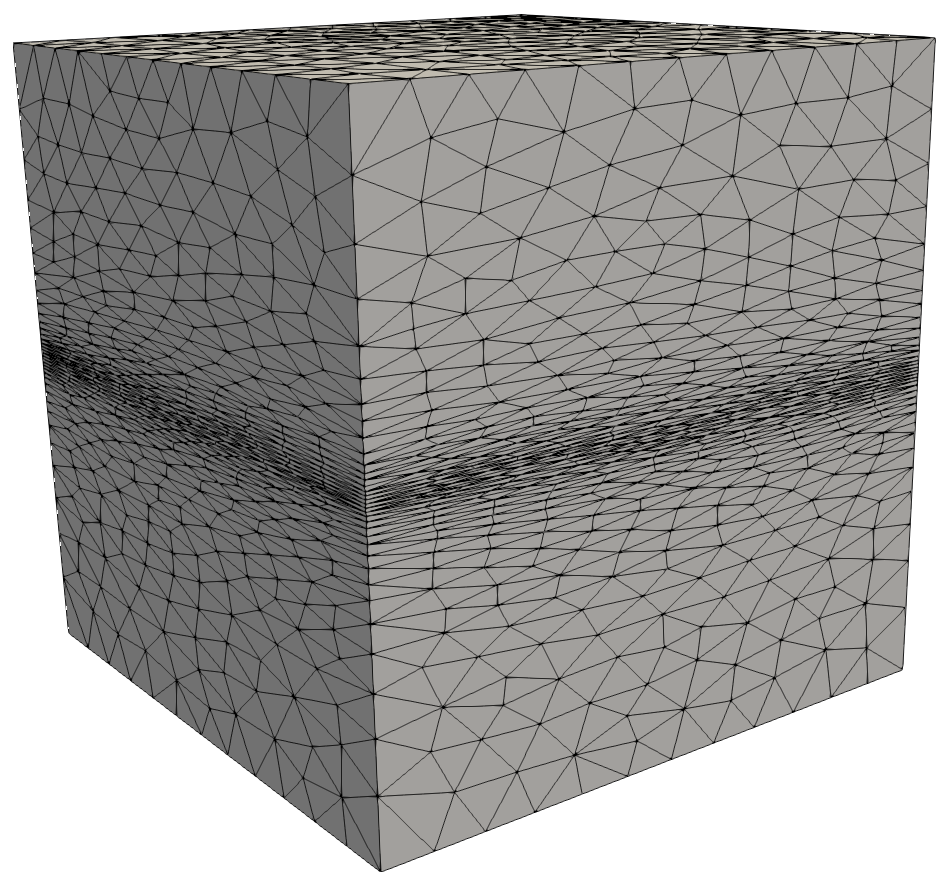
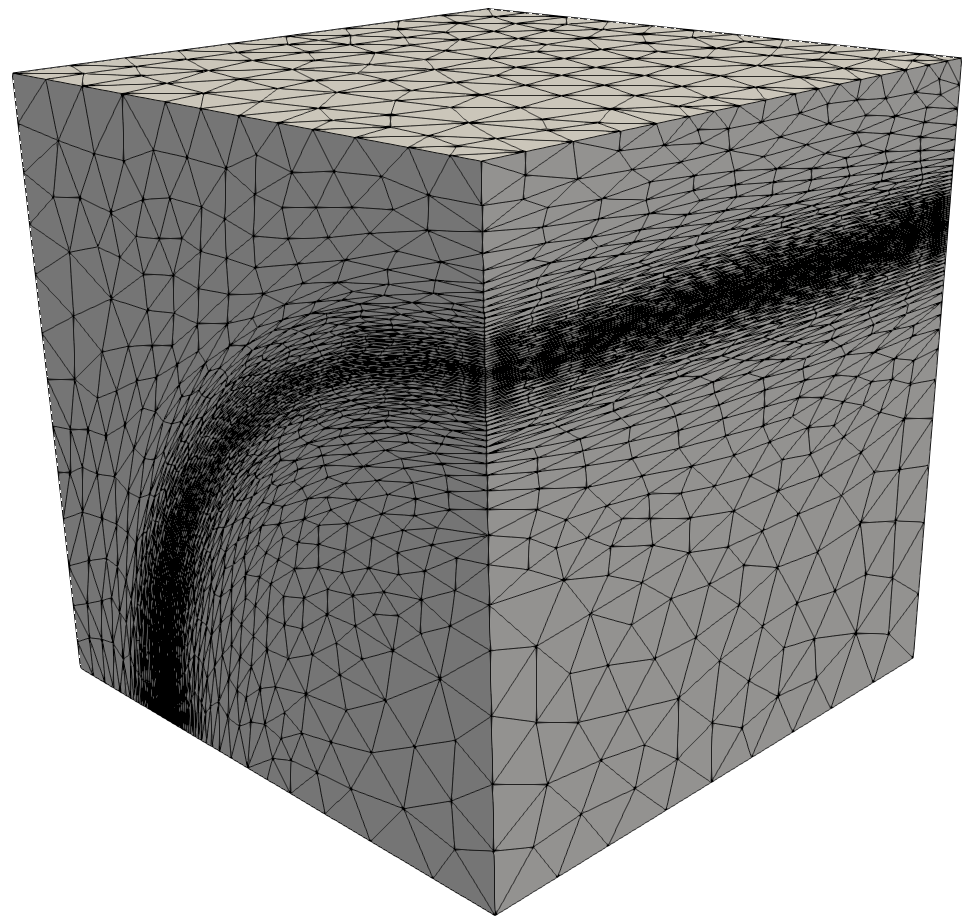
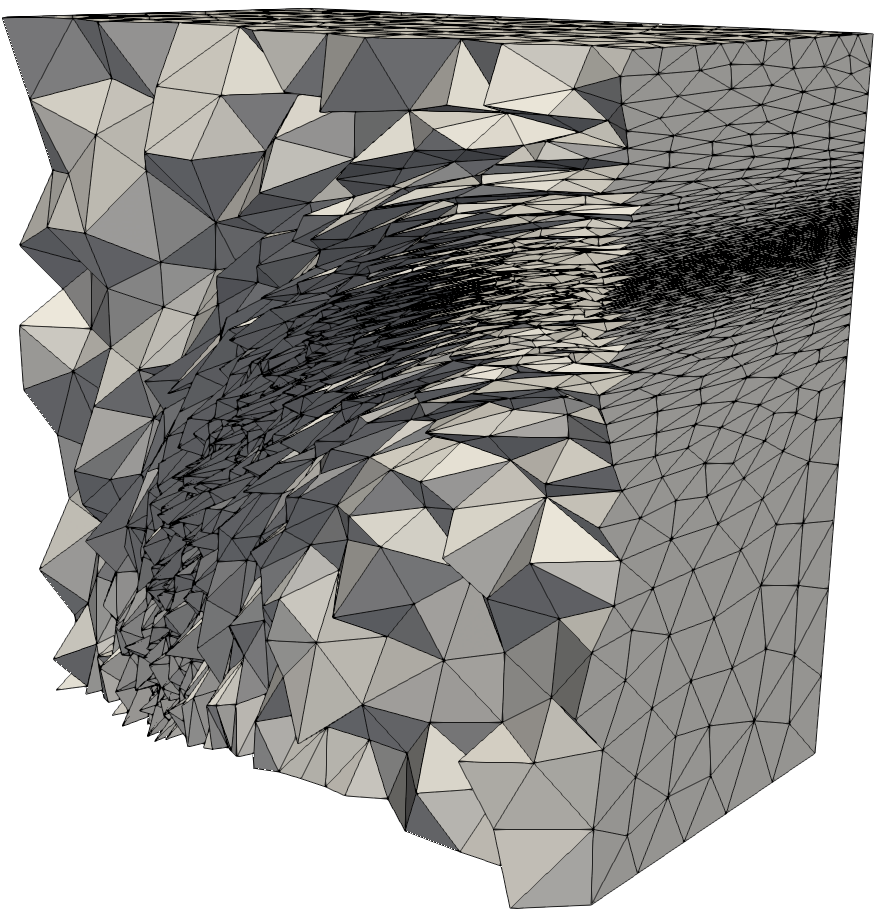
| Surface Mesh, cross-cut and detail of the generated volume mesh. | ||
|---|---|---|
|
|
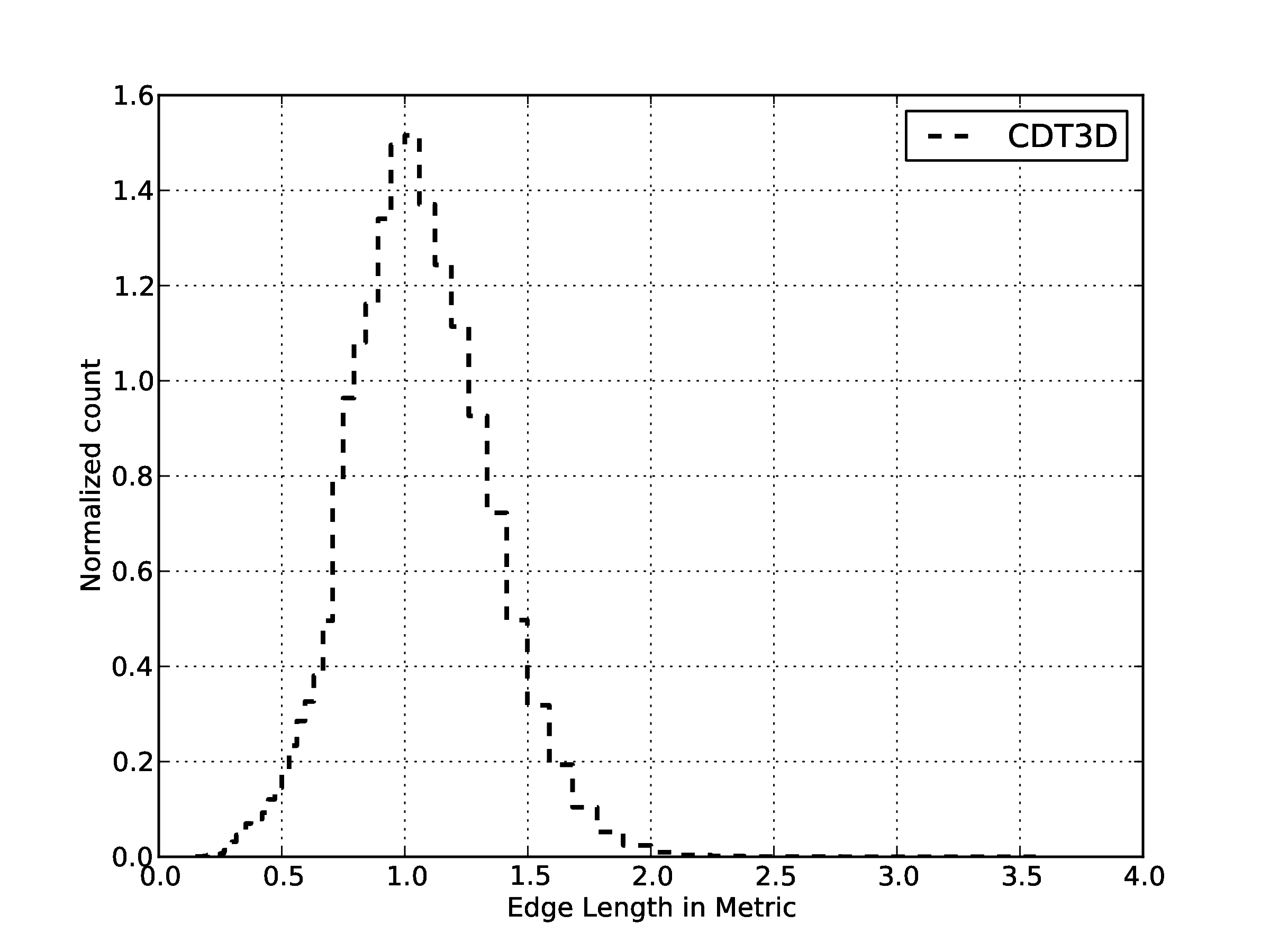
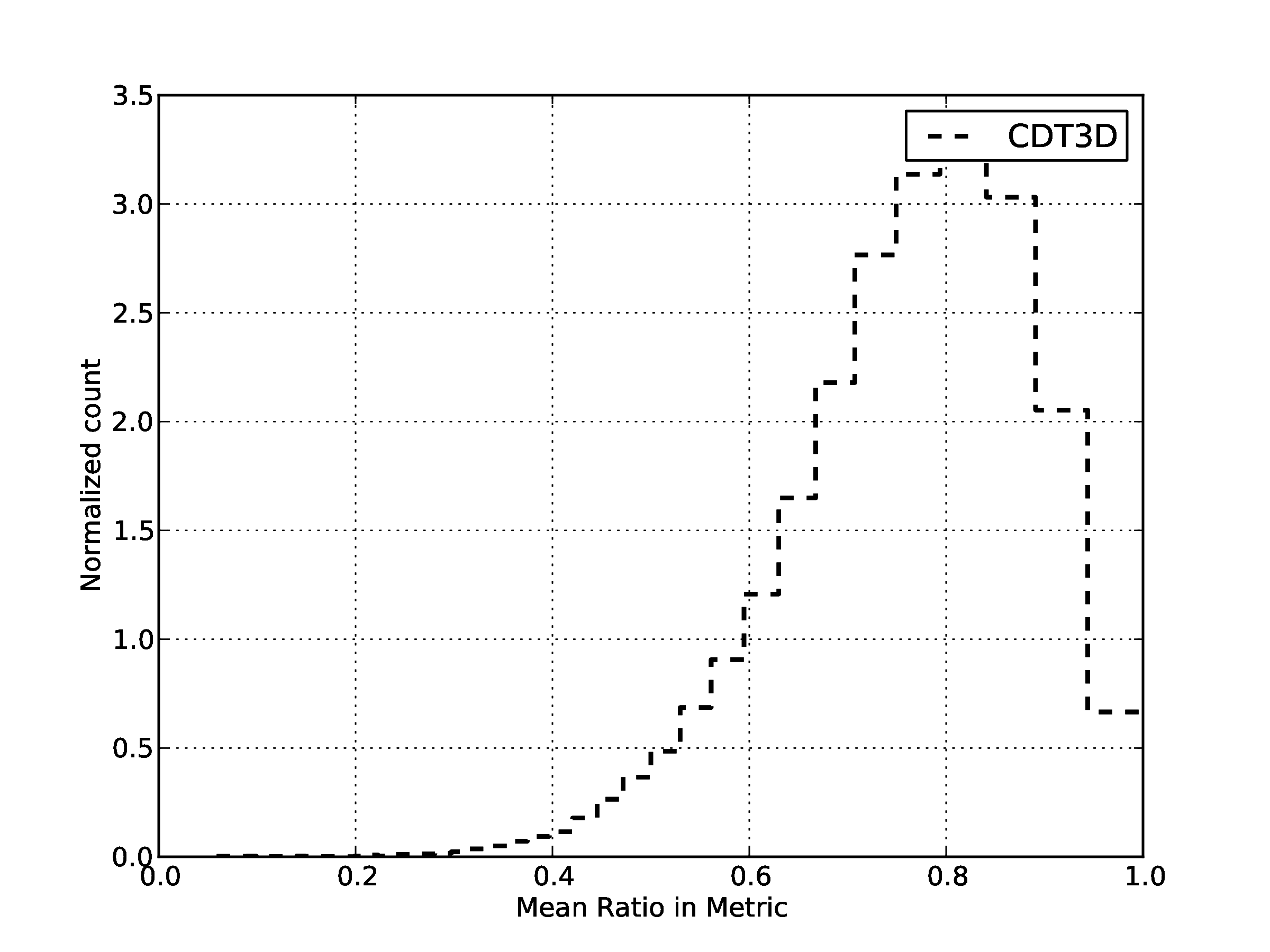
| Quality statistics in the metric space for generated volume mesh.94 % of the edges has length between [0.5,1.5].
For the mean ratio 96%,of the elements have quality higher that 0.7. | |
|---|---|
Quarter of a Cylinder
where hx = min(0.002 5^a, hmax), hy = min(0.05 · 2a, hmax), hz= hmax, hmax = 0.1, θ = arctan(x,y), a = 10 · | 0.75 - √ (x2+ y2) |
|
|

|
| Surface Mesh, cross-cut and detail of the generated volume mesh. | ||
|---|---|---|
|
|
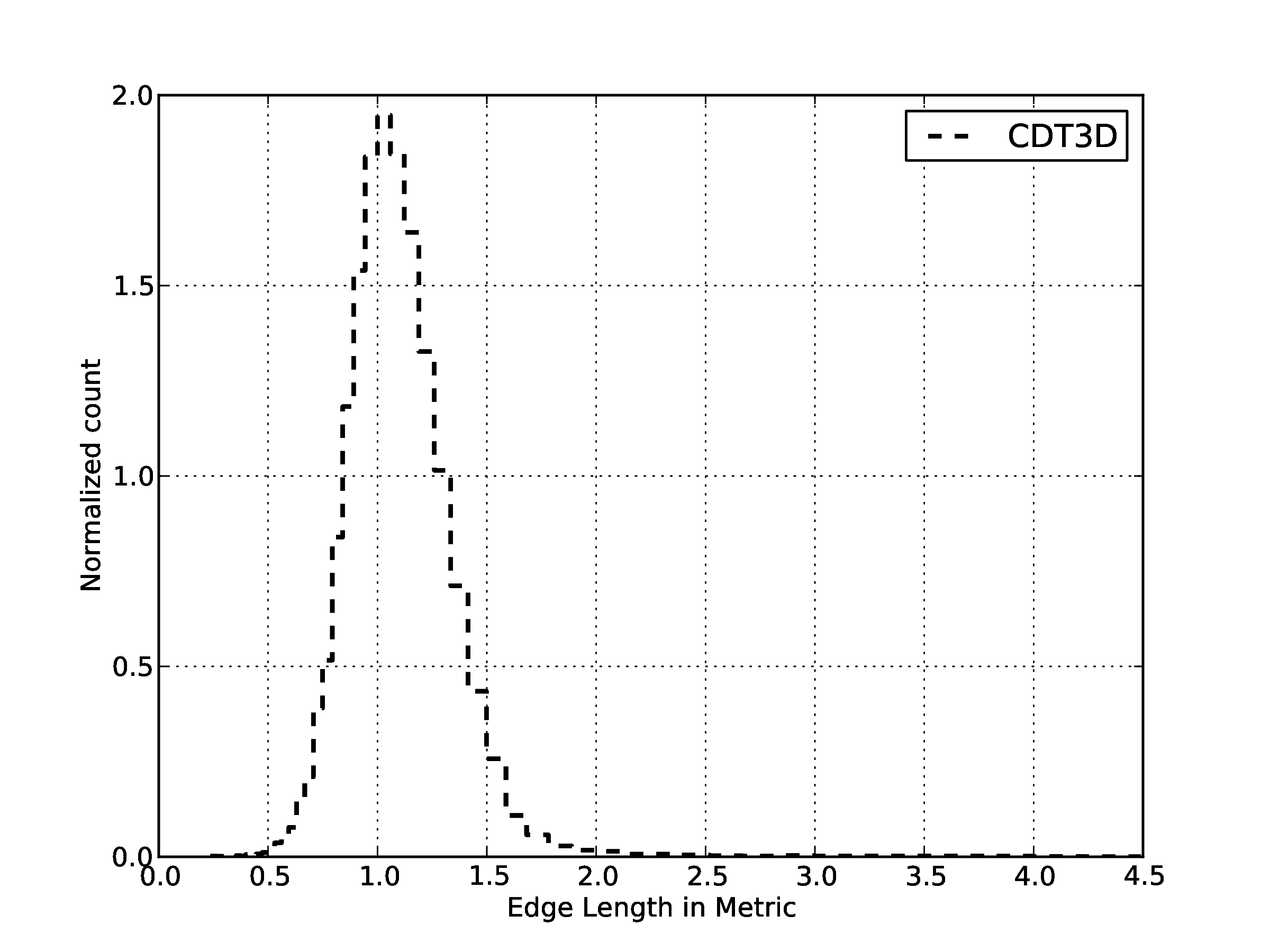
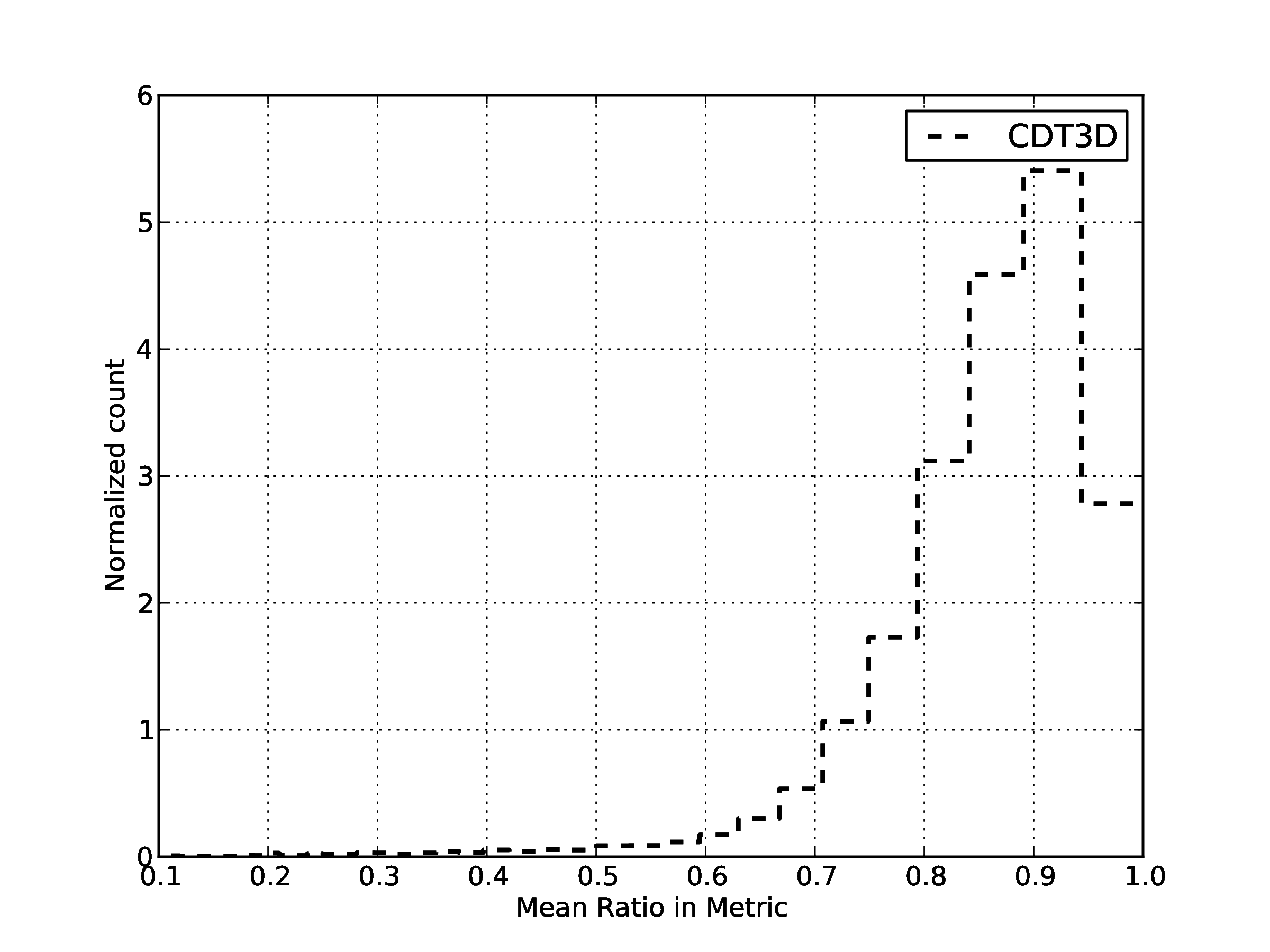
| Quality statistics in the metric space for generated volume mesh.
91 % of the edges has length between [0.5,1.5]. For the mean ratio 79% of the elements have quality higher that 0.7. | |
|---|---|
Solution Based Adaptation
Onera M6
30K Complexity
Surface and background meshes were acquired from UGAWG repository

|

|
| Initial surface mesh acquired from [1] | Refined surface mesh using as a 30K complexity background mesh acquired from [2] |

|

|
| cross cuts of the final mesh | |
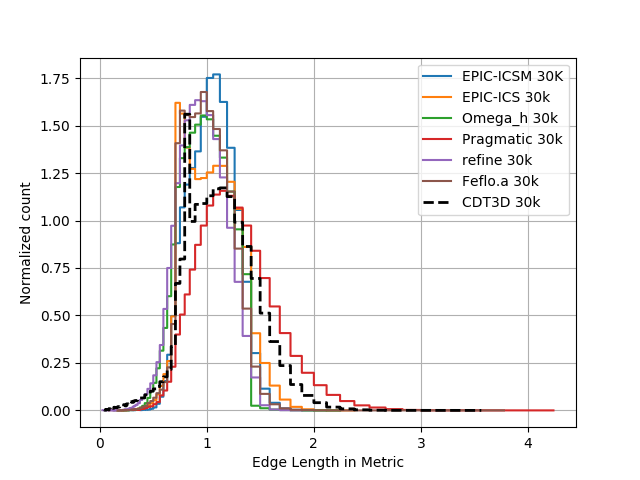
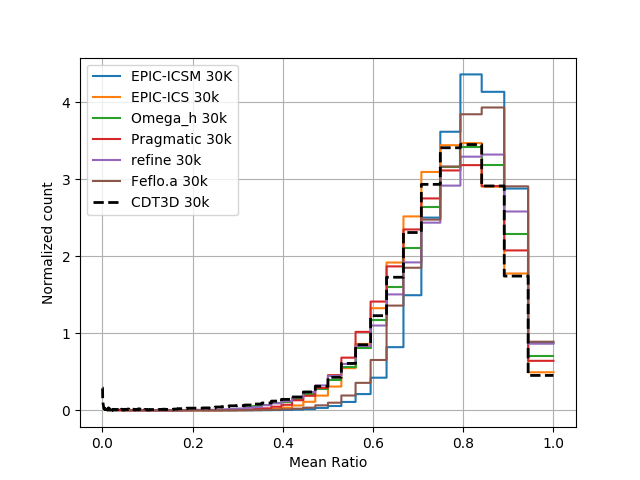
The final mesh (available here ) was compared against the results from the 2018 Scitech paper Unstructured Grid Adaptation and Solver Technology for Turbulent Flows
available at https://arc.aiaa.org/doi/abs/10.2514/6.2018-1103 .
|
|
50K Complexity
Same input surface but with different metric complexity :

|

|
| cross cuts of the final mesh | |
The background mesh is available here
The final mesh (available here )