PDR.TetGen
Contents
- 1 Parallel Delaunay Refinement (PDR) With TetGen
- 1.1 Overview
- 1.2 Compiling PDR (Shared Memory Release)
- 1.3 Compiling PDR (Initial MPI Release)
- 1.4 Using PDR (Shared Memory Manual Page)
- 1.5 Running PDR (Shared Memory Sample Execution)
- 1.6 Using PDR (MPI Manual Page)
- 1.7 Running PDR (MPI Sample Execution)
- 1.8 Heterogeneous Data (Sample Mesh)
Parallel Delaunay Refinement (PDR) With TetGen
Overview
The goal of this project is the development of a parallel mesh generator using CRTC’s PDR theory, which mathematically guarantees the following mesh generation requirements:
- Stability: the quality of the mesh generated in parallel must be comparable to that of a mesh generated sequentially. The quality is defined in terms of the shape of the elements (using a chosen space-dependent metric), and the number of the elements (fewer is better for the same shape constraint).
- Robustness: the ability of the software to correctly and efficiently process any input data. Operator intervention into a massively parallel computation is not only highly expensive, but most likely infeasible due to the large number of concurrently processed sub-problems.
- Code re-use: a modular design of the parallel software that builds upon a previously designed sequential meshing code, such that it can be replaced and/or updated with a minimal effort. Due to the complexity of meshing codes, this is the only practical approach for keeping up with the ever-evolving sequential algorithms.
- Scalability: the ratio of the time taken by the best sequential implementation to the time taken by the parallel implementation. The speedup is always limited by the inverse of the sequential fraction of the software, and therefore all non-trivial stages of the computation must be parallelized to leverage the current architectures with millions of cores.
The design and implementation of a sequential industrial strength code is labor intensive, it takes about 100 man-years. Parallel mesh generation code is even more labor intensive (by an order of magnitude for traditional parallel machines and expected to be higher for current and emerging architectures due to multiple memory and network hierarchies, fault-tolerance and power aware issues); however, because of the underlying theory that allows code re-use, this initial parallel implementation was achieved in less than six months with impressive functionality, i.e., the same as the sequential TetGen code.
The general idea of Delaunay refinement is based on the insertion of additional (Steiner) points inside the circumdisks of poor quality elements, which causes these elements to be destroyed, until they are gradually eliminated and replaced by better quality elements. It has been proven that this algorithm terminates by producing a mesh with guaranteed bounds on radius-edge ratio and on the density of elements. The main concern when parallelizing Delaunay refinement algorithms is the compatibility (i.e., data dependence) between Steiner points concurrently inserted by multiple threads or processes. Two points are Delaunay-independent if they can be safely inserted concurrently. PDR is based on overlapping the mesh with an octree, defining buffer zones around each leaf of the octree, and proving that points inserted outside the buffer zone of a leaf are always Delaunay-independent with respect to any points inserted inside this leaf.
There are two approaches to PDR, progressive and non-progressive, both of which rely on octree (data) decomposition in order to mathematically guarantee element quality and termination of the PDR algorithm for uniform isotropic Delaunay-based methods.
PDR is used with TetGen 1.4 which can be found here.
The PDR source code is provided as a compressed tar archive, which is available here. It can be extracted using the tar utility.
-
tar xvzf PDR-buildnumber.tar.gz
-
After extracting PDR, cd into the PDR directory. To perform an out-of-source-build, create a compilation directory.
-
mkdir build
-
cd build
-
Run cmake followed by make.
-
cmake ..
-
make
-
Two executables will be created:
- pdr: non-progressive pdr
- pdr_p: progressive pdr
Tool Configuration on Linux
PDR requires g++ 4.7 or higher and cmake. Both utilties, can be installed with the package manger for your Linux distribution (e.g., apt-get for Ubuntu and yum on CentOS).
Compilation has been performed and tested on CentOS with g++ version 4.9, Ubuntu with g++ versions 4.8.4, 4.9, and 5.3.1.
Tool Configuration on OSX
PDR requires g++ 4.7 or higher and cmake. CMake configuraiton and installation official instructions are provided by Kitware. If the CMake GUI is already installed in the /Applications directory, the command line tool can be activated by running
-
sudo "/Applications/CMake.app/Contents/bin/cmake-gui" --install
-
The gcc compiler included with xcode is an earlier version. The gcc47 package can be installed using the macports framework.
Compiling PDR (Initial MPI Release)
The PDR source code is provided as a compressed tar archive, which is available here. It can be extracted using the tar utility.
-
tar xvzf PDR-buildnumber.tar.gz
-
After extracting PDR, cd into the PDR directory. To perform an out-of-source-build, create a compilation directory.
-
mkdir build
-
cd build
-
Run cmake followed by make.
-
cmake ..
-
make
-
One executable will be created:
- pdr: non-progressive pdr
Tool Configuration on Linux
Compilation requires cmake and version 4.9.3 of the g++ compiler and openmpi 2.0.1 or higher.
Running PDR without flags or arguments will display the following usage message:
- Usage: ./pdr -i [inputfilename]
- -i -> Specify an input poly file (required)
- -o -> Specify a base output filename
- -s -> Specify a statistics output filename
- --grading -> Specify a uniform upper bound for circumradii
- --initial-depth -> Specify a depth limit for the initial octree
- --max-depth -> Specify a maximum depth for the final octree (progressive mode)
- --scale -> Specify the factor by which to scale the octree root
- --nooutmesh -> Suppress output of node and ele files
- --nooutoctree -> Suppress output of the generated octree
Input & Output
PDR requires that the –i flag be used to specify an input geometry.
-
./pdr –i cube.poly
-
By default, the base output filename will default to outputMesh. This can be overridden with the –o flag.
-
./pdr –i cube.poly –o refinedCube
-
This will result in three files, refinedCube.node, refinedCube.ele, and refinedCube-octree.vtk. The first two files contain the points and tetrahedra, respectively. The third file contains the final octree.
Mesh or octree output can be suppressed with --nooutmesh and --nooutoctree, respectively.
Input File Format
PDR accepts input as PLCs in the poly file format as described in the TetGen documentation with three restrictions:
- No leading comments can be present.
- The first line must contain 4 integers.
- If no holes are present, the optional holes section must be included with a 0.
The unit cube is provided as an example in cube.poly. The poly file must not contain any leading comments.
This page describes both the use of the shared memory PDR release and the results for four example geometries:
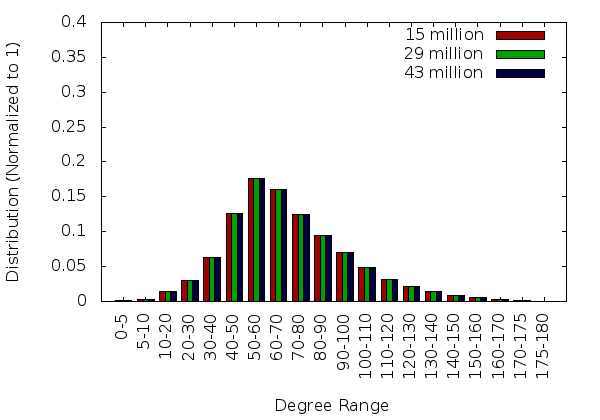
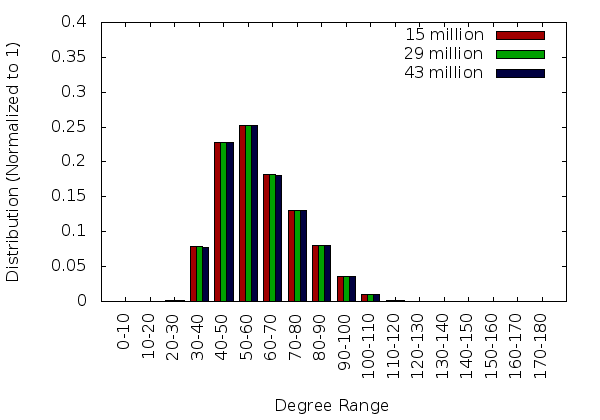
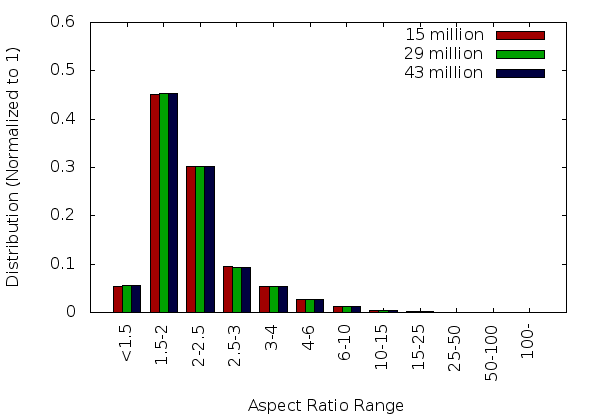
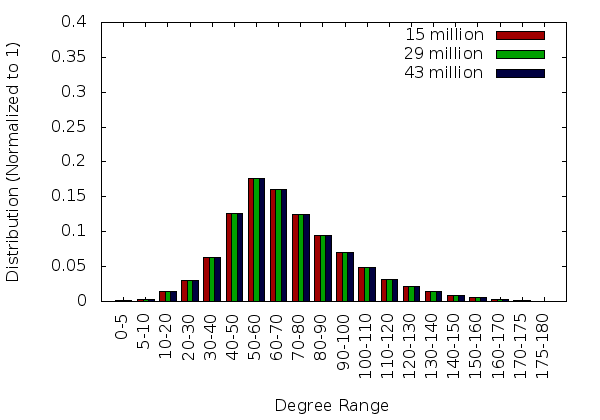
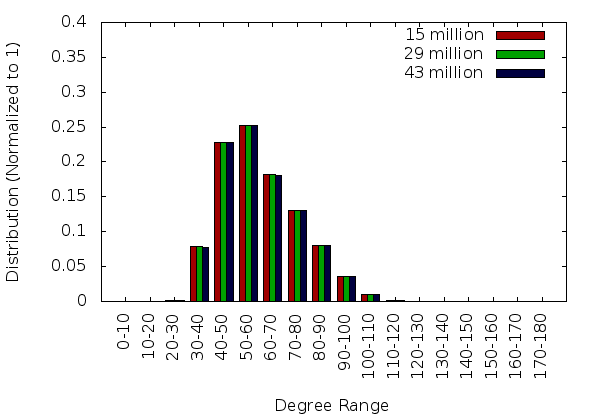
The mesh quality statitstics, shown in the graphs on the remainder of this page, were generated by reconstructing the mesh with Tetgen. Future versions of PDR will generate the statistics natively when the correct command line arguments are provided.
Unit Cube
When run on the unit cube using the following command:
-
./pdr -p 4 -s statistics.txt --grading 0.015 --initial-depth 4 -i cube.poly
-
PDR will generate a mesh of approximately 2 million tetrahedra using four cores. Four files will be generated:
- output.node - Listing of all vertices - Note that this file is output as a text file. The version provided here is compressed into a zip file.
- output.ele - Listing of all tetrahedra - Note that this file is output as a text file. The version provided here is compressed into a zip file.
- output-octree.vtk - Listing of the final octree in VTK format - This is compressed into a zip file.
- statistics.txt - Listing of time statistics - Note that these times will vary based on hardware.
- Note: Some of the above files are large. Each of them can be opened in a text editor.
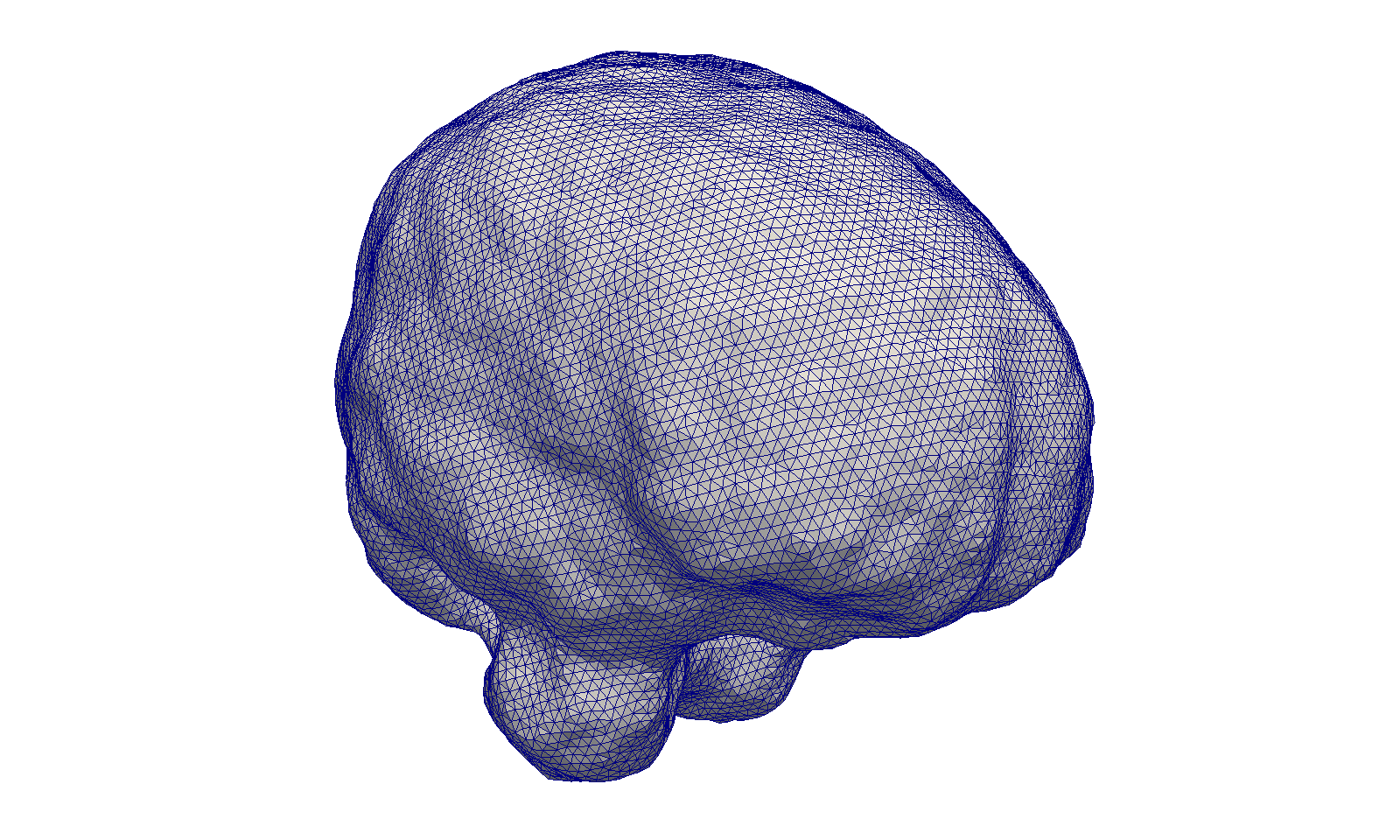
Brain
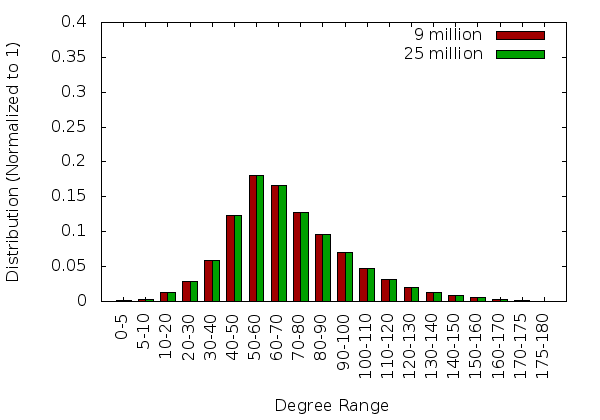
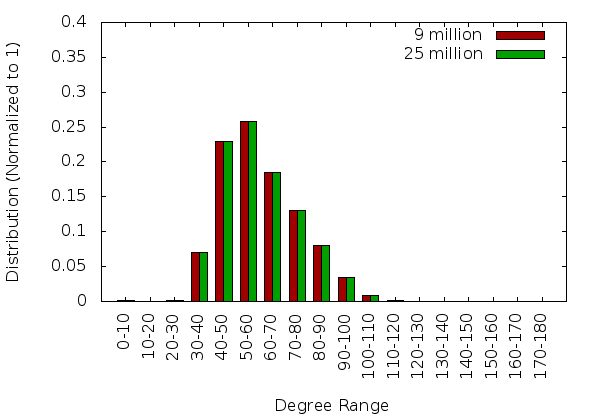
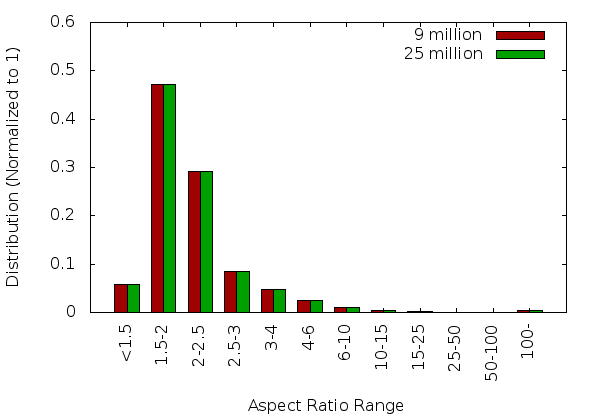
This section describes the results obtained from the brain_cbc3d geometry for a single core and 32 cores.
Input Mesh
Command for Single Core Execution
-
./pdr -p 1 -s pdr-np-01-1.0-depth-04-06-brain_CBC3D.txt --grading 1.0 --initial-depth 4 -o pdr-np-01-1.0-depth-04-06-brain_CBC3D
-
Command for 32 Core Execution
- ./pdr -p 32 -s pdr-np-32-1.0-depth-04-06-brain_CBC3D.txt --grading 1.0 --initial-depth 4 --max-depth 6 -o pdr-np-32-1.0-depth-04-06-brain_CBC3D
Argument Settings Used
- -p 1 - set the number of cores
- -s pdr-np-01-1.0-depth-04-06-brain_CBC3D.txt - set the file name for time statistic output
- --grading 1.0 - set the grading
- --initial-depth 4 - set the initial octree depth
- --max-depth 6 - set the maximum octree depth (ignored in non-progressive mode)
- -o pdr-np-01-1.0-depth-04-06-brain_CBC3D - set the base output file name
- -i brain_CBC3D.poly - set the input file
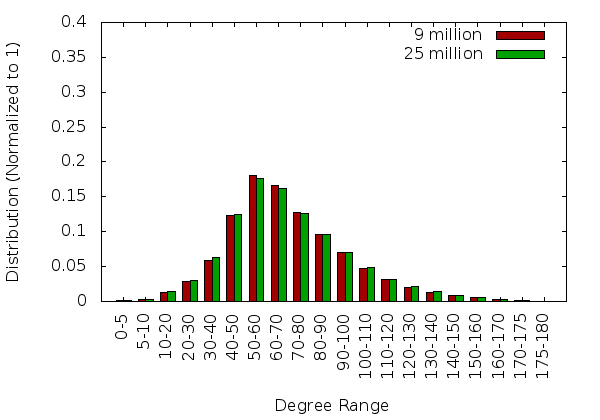
Single Core Statistics
32 Core Statistics
Socket
This section describes the results obtained from the socket geometry for a single core and 32 cores.
Input Mesh
Command for Single Core Execution
- ./pdr -p 1 -s pdr-np-01-1.0-depth-04-06-socket.txt --grading 1.0 --initial-depth 4 --max-depth 6 -o pdr-np-01-1.0-depth-04-06-socket -i socket.poly
Command for 32 Core Execution
- ./pdr -p 32 -s pdr-np-32-1.0-depth-04-06-socket.txt --grading 1.0 --initial-depth 4 --max-depth 6 -o pdr-np-32-1.0-depth-04-06-socket -i socket.poly
Argument Settings Used
- -p 1 - set the number of cores
- -s pdr-np-01-1.0-depth-04-06-socket.txt - set the file name for time statistic output
- --grading 1.0 - set the grading
- --initial-depth 4 - set the initial octree depth
- --max-depth 6 - set the maximum octree depth (ignored in non-progressive mode)
- -o pdr-np-01-1.0-depth-04-06-socket - set the base output file name
- -i socket.poly - set the input file
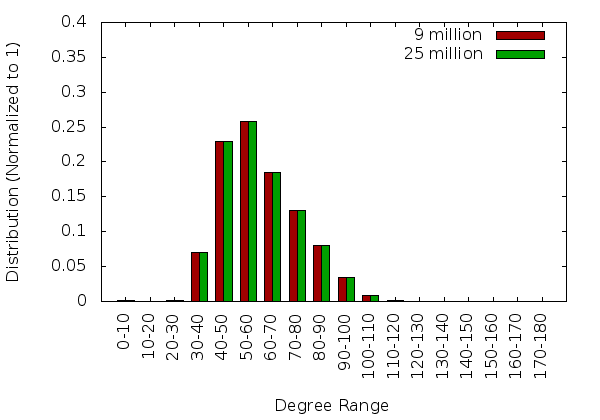
Single Core Statistics
32 Core Statistics
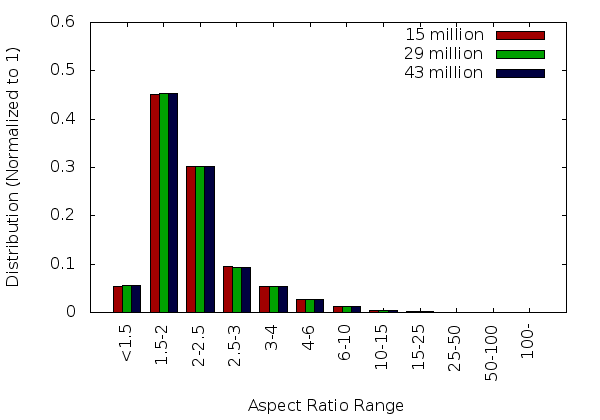
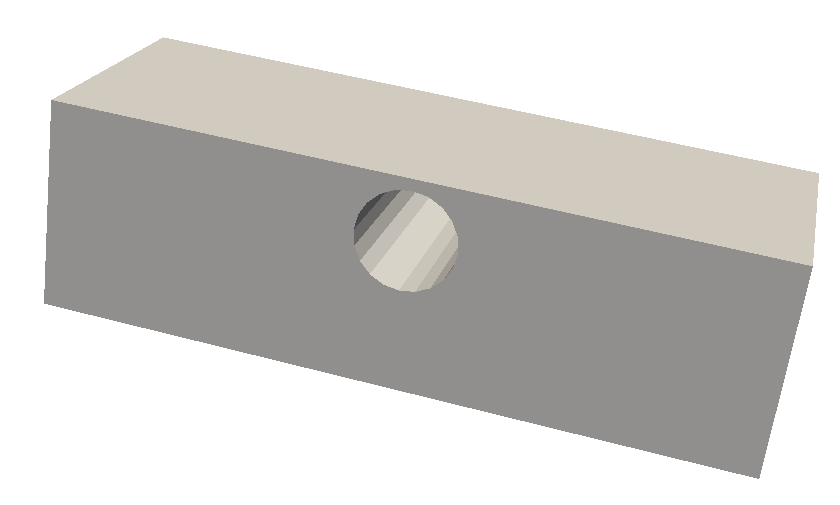
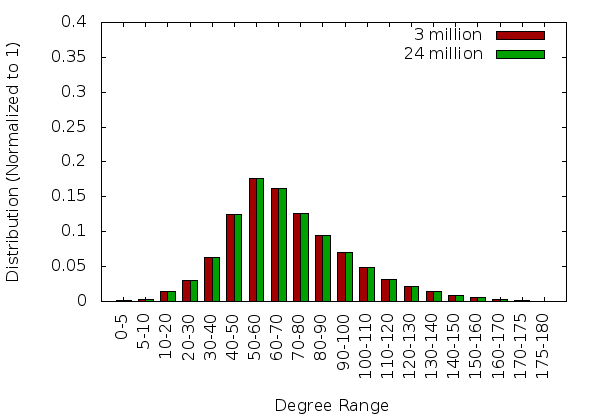
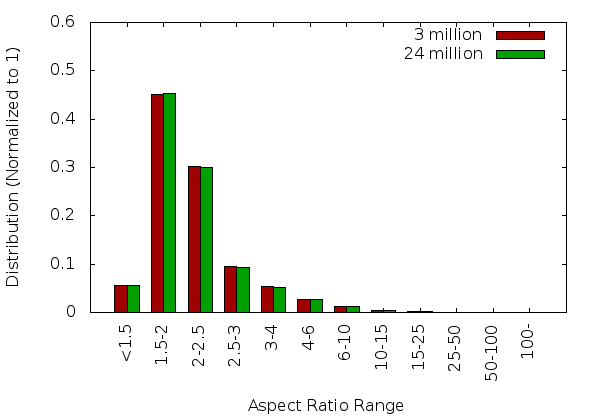
Bar3
This section describes the results obtained from the bar3 geometry for a single core and 32 cores.
Input Mesh
Command for Single Core Execution
- ./pdr -p 1 -s pdr-np-01-0.03-depth-04-06-bar3.txt --grading 0.03 --initial-depth 4 --max-depth 6 -o pdr-np-01-0.03-depth-04-06-bar3 -i bar3.poly
Command for 32 Core Execution
- ./pdr -p 32 -s pdr-np-32-0.03-depth-04-06-bar3.txt --grading 0.03 --initial-depth 4 --max-depth 6 -o pdr-np-32-0.03-depth-04-06-bar3 -i bar3.poly
Argument Settings Used
- -p 1 - set the number of cores
- -s pdr-np-01-0.03-depth-04-06-bar3.txt - set the file name for time statistic output
- --grading 0.03 - set the grading
- --initial-depth 4 - set the initial octree depth
- --max-depth 6 - set the maximum octree depth (ignored in non-progressive mode)
- -o pdr-np-01-0.03-depth-04-06-bar3 - set the base output file name
- -i bar3.poly - set the input file
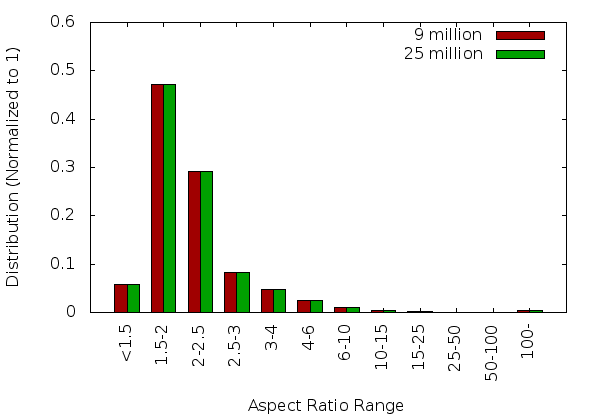
Single Core Statistics
32 Core Statistics
Using PDR (MPI Manual Page)
This page describes the available command line arguments, input format, and output files for the intial MPI release of PDR with TetGen.
Current alpha version of MPI PDR Release works only with the unit cube and bar3 geometries!
Running PDR without flags or arguments will display the following usage message:
- Usage: mpirun -np [numberofnodes] pdr -i [inputfilename]
- -i -> Specify an input poly file (required)
- --grading -> Specify a uniform upper bound for circumradii
- --initial-depth -> Specify a depth limit for the initial octree
Input & Output
PDR requires that the –i flag be used to specify an input geometry.
- mpirun -np 8 pdr –i cube.poly
By default, the base output filename will default to outputMesh.
This will result in three files, outputMesh.node, outputMesh.ele, and outputMesh-octree.vtk. The first two files contain the points and tetrahedra, respectively. The third file contains the final octree.
Input File Format
PDR accepts input as PLCs in the poly file format as described in the TetGen documentation with three restrictions:
- No leading comments can be present.
- The first line must contain 4 integers.
- If no holes are present, the optional holes section must be included with a 0.
Running PDR (MPI Sample Execution)
This page describes both the use of the initial MPI release of PDR with TetGen and the results for two example geometries:
Current alpha version of MPI PDR Release works only with the unit cube and bar3 geometries!
Unit Cube
When run on the unit cube using the following command:
- mpirun -np 8 pdr --grading 0.015 --initial-depth 3 -i cube.poly
PDR will generate a mesh of approximately 2 million tetrahedra using eight nodes. The following shows the resulting mesh.
Bar3
This section describes the results obtained from the bar3 geometry when run on 16 nodes.
Input Mesh
Command for 16-node Execution
- mpirun -np 16 pdr --grading 0.015 --initial-depth 3 -i bar3.poly
Argument Settings Used
- --grading 0.015 - set the grading
- --initial-depth 3 - set the intial octree depth
- -i bar3.poly - set the input file
The following shows the resulting mesh.