Difference between revisions of "Reproducibility TetGen"
(Created page with "In the past we introduced four criteria for the successful implementation of industrial strength, scalable parallel mesh generation: (i) stability, (ii) robustness, (iii) code...") |
m (Ctsolakis moved page Reproducibility.TetGen to Reproducibility TetGen) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 45: | Line 45: | ||
|[[Image:Tetgen_reproducibility1.png|500px|link=]] | |[[Image:Tetgen_reproducibility1.png|500px|link=]] | ||
|- | |- | ||
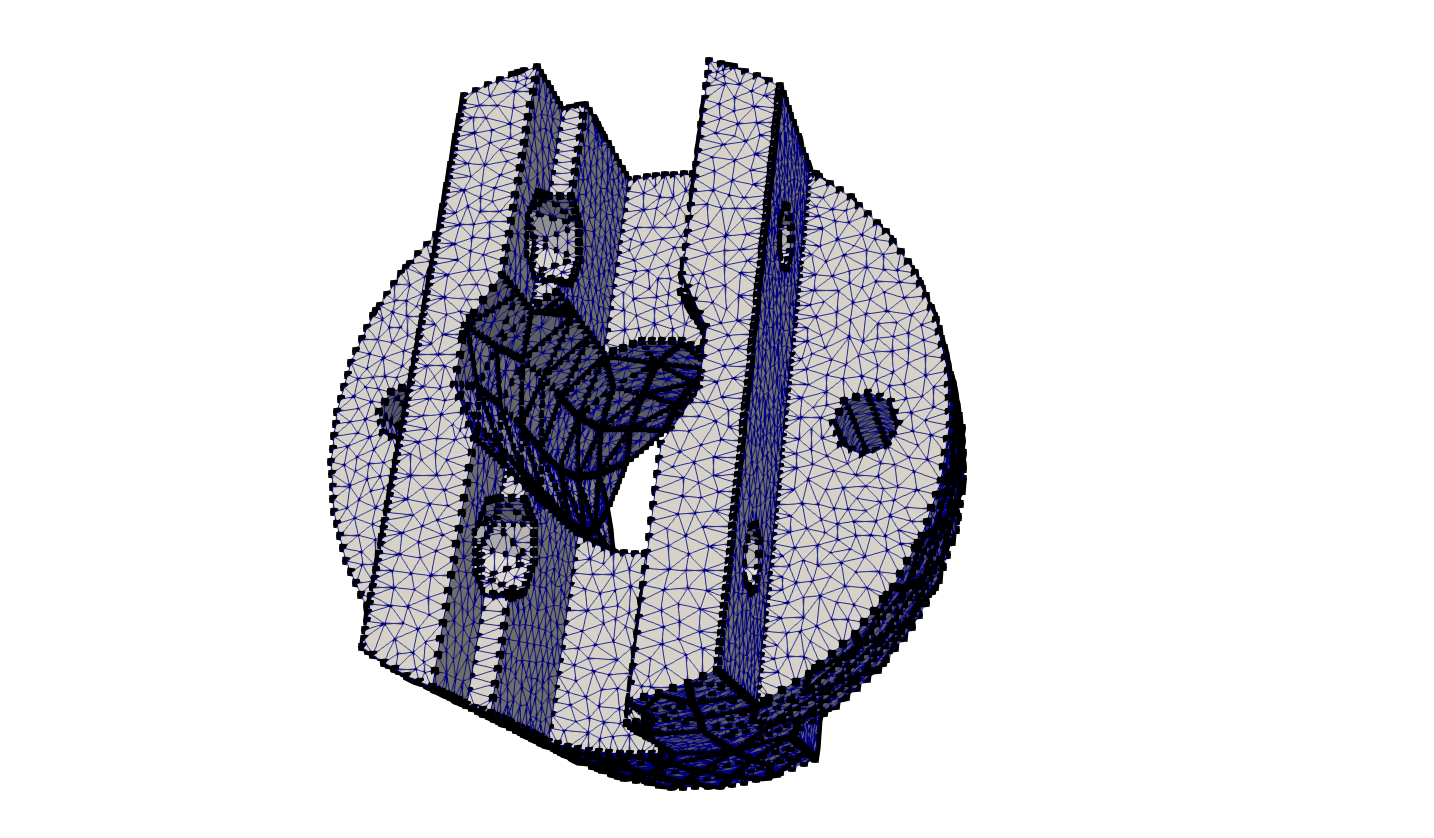
| − | |'''Figure 1 :''' Coarse mesh of the socket geometry. Black dots represent points where TetGen reports errors. | + | |'''Figure 1 :''' Coarse mesh of the socket geometry. <br> Black dots represent points where TetGen reports errors. |
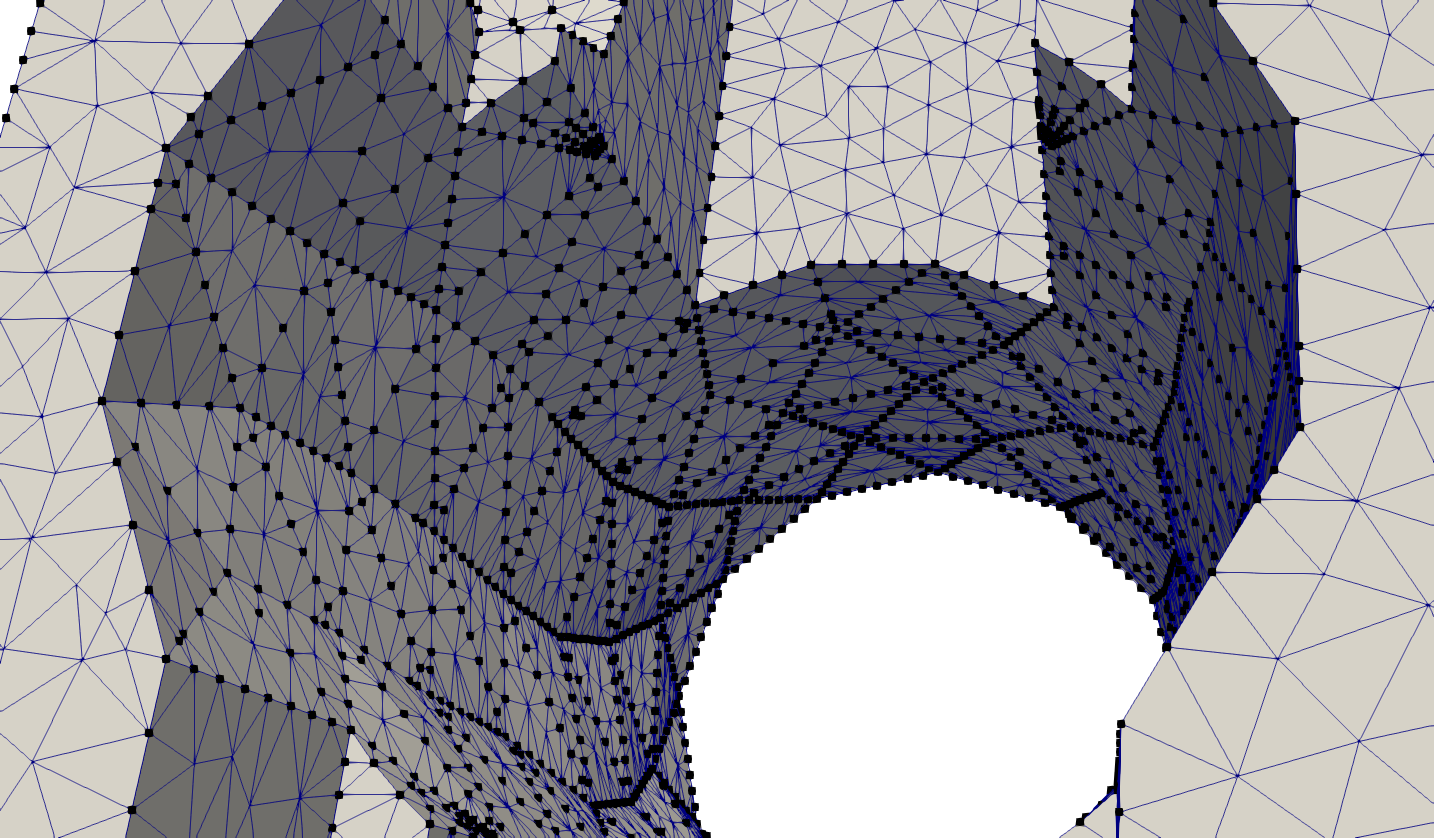
|'''Figure 2 :''' Zoom-in view of the center of the socket | |'''Figure 2 :''' Zoom-in view of the center of the socket | ||
|} | |} | ||
Latest revision as of 09:46, 29 March 2018
In the past we introduced four criteria for the successful implementation of industrial strength, scalable parallel mesh generation: (i) stability, (ii) robustness, (iii) code re-use and (iv) scalability.
However, our recent experience with distributed memory implementation of PDR framework using TetGen exposed an underline issue (strong and weak reproducibility) that is not apparent in shared memory implementations. The reproducibility issue (for precise definition see below) depends on the underline sequential mesh generation code used to maximize code re-use. In the specific case TetGen. Studies to evaluate AFLR with respect to reproducibility will be completed soon.
When using TetGen over PDR’s distributed memory implementation (i.e., using MPI) we need to be able to reconstruct a mesh out of a set of points and tetrahedral, in order words we need to populate the data structures of TetGen in order to continue refining the leaf from where it was left before.
Although, this capability exists as a function in TetGen ( tetgenmesh::reconstruct() ) the reconstruction procedure is not robust enough even for simple inputs. To justify the need for reproducibility argument one can create a coarse mesh of the socket geometry (one of the four geometries used in earlier PETTT report and is part of TetGen’s benchmark) using TetGen 1.5.0 (the most recent and advanced version) and then pass as an input the set of points and tetrahedra that was produced back to TetGen . TetGen reports many errors about wrong segment connections and aborts after few seconds with the following error:
Reconstructing mesh ...
Checking consistency of mesh... In my studied opinion, the mesh appears to be consistent. Checking consistency of the mesh boundary... Mesh boundaries connected correctly. Checking tet->seg connections... Checking seg->tet connections... Checking seg->seg connections... !! Wrong seg-seg connection at point 41. . . . !! Wrong seg-seg connection at point 16133. !! !! !! !! Found 2363 missing connections. Checking Delaunay property of the mesh... The mesh is Delaunay.
Mesh reconstruction seconds: 0.456937 Refining mesh... tetgen: ../src/tetgen.cxx:4884: double tetgenmesh::insphere_s(double*, double*, double*, double*, double*): Assertion `oriB != 0.0' failed.
This is a generic error due to wrong initialization in any of the core data structures. TetGen provides functions that test the integrity of the internal data structures. Enabling these functions and visualizing the information reveals that at 2363 out of the 10472 boundary points the tetgenmesh::reconstructmesh() procedure did not linked the segments appropriately. Even by passing more information to the aforementioned function, that is, boundary edge and boundary face connectivity the final result is the same.
The reproducibility criterion is not required for shared memory PDR implementations, since the mesh is not reconstructed at any leaf during the refinement instead, PDR access the mesh directly.
In conclusion, because of this problem and intensive debugging and thinking we come up with the following two definitions and a fifth criterion for parallel mesh generation:
Strong Reproducibility requires termination of the mesh generation algorithm the output mesh should be identical to the input mesh.
Weak Reproducibility requires termination of the mesh generation algorithm the output mesh should have the same quality as the input mesh.
|
|
| Figure 1 : Coarse mesh of the socket geometry. Black dots represent points where TetGen reports errors. |
Figure 2 : Zoom-in view of the center of the socket |