Difference between revisions of "PDR.AFLR"

From crtc.cs.odu.edu
Jump to: navigation, search
(→‎Overview)
(→‎Stability)
 
(5 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
= Introduction =
 
= Introduction =
 +
For the last 30 years, legacy Finite Element (FE) mesh generation methods and software were typically developed with a focus on high performance for single core architectures and without any thought towards scalability for a large number of cores. These codes are still used for production in several industries, including NASA. However, NASA’s Computational Fluid Dynamics (CFD) 2030 Vision will require those highly functional codes to run on large-scale parallel architectures. Highly optimized sequential versions of existing state-of-the-art mesh generation codes, in addition to geometric and numerical challenges imposed by the nature of mesh generation complexity, makes their parallelization a highly challenging problem. In this project, we focus on one of the top, industrial strength mesh generators, called Advancing Front Local Reconnection (AFLR), which is used by NASA, the DoD, and DoE, as well as a number of aerospace industry top research groups. AFLR has not been fully parallelized to properly utilize large-scale supercomputing hardware.
 +
== Overview ==
 +
Modifications were made to AFLR to enable its execution within the Parallel Data Refinement (PDR, a generalized version of Parallel Delaunay Refinement meant to be capable of utilizing any mesh generator, i.e. code re-use) method and software framework (specifically the non-progressive approach) while maintaining AFLR’s full functionality and providing stability i.e., ensuring that the quality of the mesh generated (from each of the individually refined subdomains) is comparable to that of a mesh generated sequentially (by serial AFLR). The quality is defined in terms of the shape and number of the elements. PDR decomposes a meshing problem by using an octree consisting of numerous leaves, or subdomains, that each hold a part of the mesh. The general idea of PDR is to concurrently refine the octree leaves while maintaining mesh conformity. This methodology is proven to generate a conforming mesh after refining the subdomains generated from an input geometry using data decomposition.
 +
 +
= Reproducibility =
 +
AFLR meets the reproducibility requirement of PDR, as it maintains weak reproducibility (which can be seen in the below example of refinement for the missile geometry). More examples are shown [[Reproducibility_AFLR | here]].
 +
<div><ul>
 +
<li style="display: inline-block;"> [[File: missile1.png|thumb|none|250px]] </li>
 +
<li style="display: inline-block;"> [[File: missile_reproducibility_test.png|thumb|none|650px]] </li>
 +
</ul></div>
 +
 +
= Stability =
 +
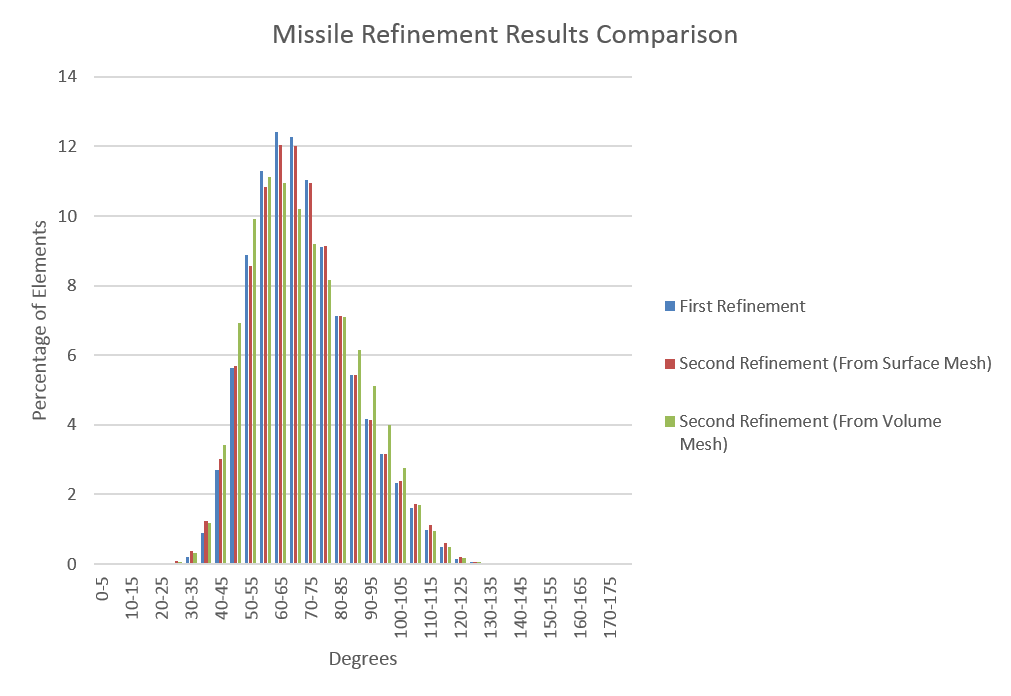
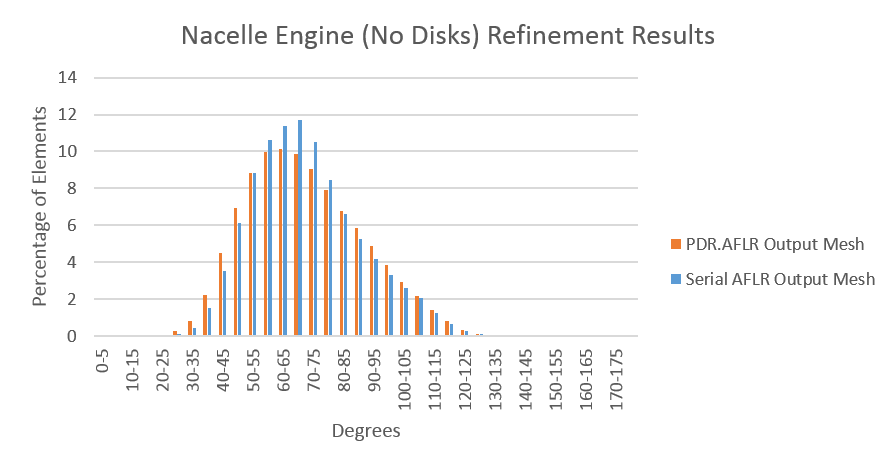
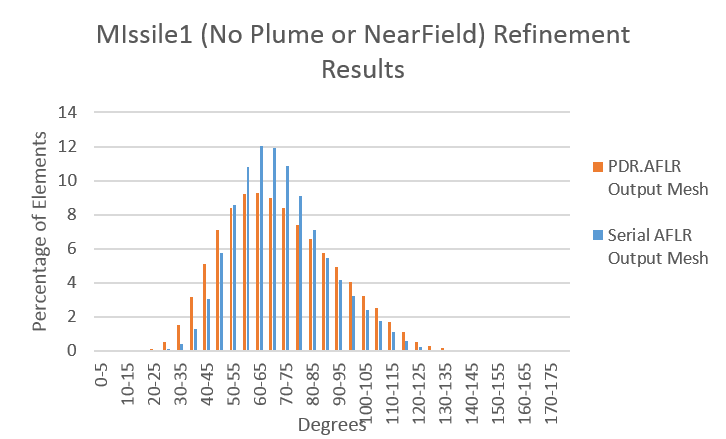
Preliminary results from the initial implementation of the sequential, data-decomposed AFLR show that PDR’s data decomposition does not hinder the quality of the output as it can be seen from the below quality statistics of meshes in comparison to their quality when generated by the serial AFLR. The bar charts show that while the output meshes of the modified AFLR contain slightly more elements of lower quality (percentage of elements towards both ends of the charts), it maintains its stability with a close number of high quality elements to that of the serial AFLR. This implementation is limited to the refinement of manifold, genus zero geometries and will be extended to more complex geometries to satisfy the robustness requirement of PDR in the final version of PDR.AFLR. It is also unable to refine meshes with transparent/embedded surfaces. This will also be addressed in the final version of PDR.AFLR. For simplicity, any transparent/embedded surfaces were removed from certain geometries while testing the stability of the data-decomposed AFLR. This is specified for specific geometries below.
 +
<div><ul>
 +
<li style="display: inline-block;"> [[File: nacelle_1.png|thumb|none|650px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: nacelle_2.png|thumb|none|650px|'''(b)''']] </li>
 +
<li style="display: inline-block;"> [[File: nacelle_stability_1.png|thumb|none|650px|'''(c)''']] </li>
 +
</ul></div>
 +
:The Fan and Turbine Disk surfaces were removed from the nacelle engine geometry. (a) and (b) show different viewpoints of the geometry. (c) compares the dihedral angle distributions of the output meshes between serial AFLR and PDR.AFLR.
 +
<br><br><br><br>
 +
 +
<div><ul>
 +
<li style="display: inline-block;"> [[File: missile1_1.png|thumb|none|600px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: missile1_2.png|thumb|none|600px|'''(b)''']] </li>
 +
<li style="display: inline-block;"> [[File: missile_stability_1.png|thumb|none|600px|'''(c)''']] </li>
 +
</ul></div>
 +
:The Plume and NearField embedded surfaces were removed from the missile1 geometry. (a) and (b) show different viewpoints of the geometry. (c) compares the dihedral angle distributions of the output meshes between serial AFLR and PDR.AFLR.
 +
<br><br><br><br>
  
−
== Overview ==
+
<div><ul>
−
''' TODO '''
+
<li style="display: inline-block;"> [[File: missile2.png|thumb|none|650px|'''(a)''']] </li>
−
The goal of this project is the development of a parallel mesh generator using CRTC’s PDR theory, which mathematically guarantees the following mesh generation requirements:
+
<li style="display: inline-block;"> [[File: missile2_stability_1.png|thumb|none|450px|'''(b)''']] </li>
−
:# '''Stability''': the quality of the mesh generated in parallel must be comparable to that of a mesh generated sequentially. The quality is defined in terms of the shape of the elements (using a chosen space-dependent metric), and the number of the elements (fewer is better for the same shape constraint).
+
</ul></div>
−
:# '''Robustness''': the ability of the software to correctly and efficiently process any input data. Operator intervention into a massively parallel computation is not only highly expensive, but most likely infeasible due to the large number of concurrently processed sub-problems.
+
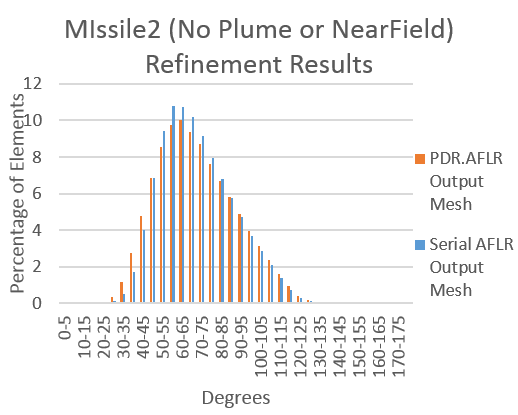
:The Plume and NearField embedded surfaces were removed from the missile2 geometry.(a) shows the modified missile2 geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
−
:# '''Code re-use''': a modular design of the parallel software that builds upon a previously designed sequential meshing code, such that it can be replaced and/or updated with a minimal effort. Due to the complexity of meshing codes, this is the only practical approach for keeping up with the ever-evolving sequential algorithms.
+
<br><br><br><br>
−
:# '''Scalability''': the ratio of the time taken by the best sequential implementation to the time taken by the parallel implementation. The speedup is always limited by the inverse of the sequential fraction of the software, and therefore all non-trivial stages of the computation must be parallelized to leverage the current architectures with millions of cores.
+
 
−
:# ''' Reproducibility ''': (weak & strong) TetGen meets none of these. For details see [LINK]. When it comes to shared memory no problem , in distributed memory (explain) This is why results are on limited geometries. 
+
<div><ul>
−
The design and implementation of a sequential industrial strength code is labor intensive, it takes about 100 man-years. Parallel mesh generation code is even more labor intensive (by an order of magnitude for traditional parallel machines and expected to be higher for current and emerging architectures due to multiple memory and network hierarchies, fault-tolerance and power aware issues); however, because of the underlying theory that allows code re-use, this initial parallel implementation was achieved in less than six months with impressive functionality, i.e., the same as the sequential TetGen code.
+
<li style="display: inline-block;"> [[File: defroster.png|thumb|none|400px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: defroster_stability_1.png|thumb|none|500px|'''(b)''']] </li>
 +
</ul></div>
 +
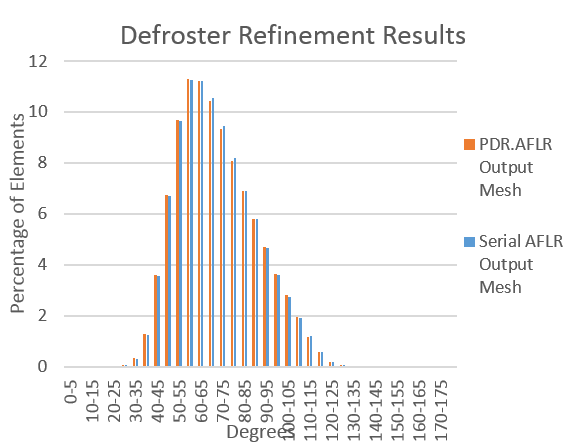
:(a) shows the defroster geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
−
The general idea of Delaunay refinement is based on the insertion of additional (Steiner) points inside the circumdisks of poor quality elements, which causes these elements to be destroyed, until they are gradually eliminated and replaced by better quality elements. It has been proven that this algorithm terminates by producing a mesh with guaranteed bounds on radius-edge ratio and on the density of elements. The main concern when parallelizing Delaunay refinement algorithms is the compatibility (i.e., data dependence) between Steiner points concurrently inserted by multiple threads or processes. Two points are Delaunay-independent if they can be safely inserted concurrently. PDR is based on overlapping the mesh with an octree, defining buffer zones around each leaf of the octree, and proving that points inserted outside the buffer zone of a leaf are always Delaunay-independent with respect to any points inserted inside this leaf.
+
<div><ul>
 +
<li style="display: inline-block;"> [[File: rocket_AFLR.png|thumb|none|250px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: rocket_stability_1.png|thumb|none|500px|'''(b)''']] </li>
 +
</ul></div>
 +
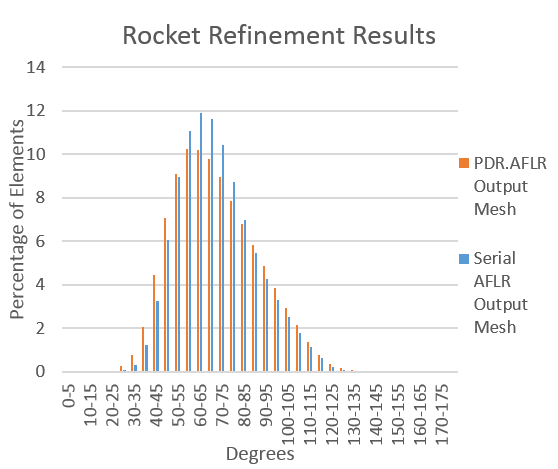
:(a) shows the rocket geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
−
There are two approaches to PDR, progressive and non-progressive, both of which rely on octree (data) decomposition in order to mathematically guarantee element quality and termination of the PDR algorithm for uniform isotropic Delaunay-based methods.
+
<div><ul>
 +
<li style="display: inline-block;"> [[File: dome.png|thumb|none|650px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: dome_stability_1.png|thumb|none|450px|'''(b)''']] </li>
 +
</ul></div>
 +
:(a) shows the dome geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
−
PDR is used with TetGen 1.4 which can be found [http://wias-berlin.de/software/tetgen/ here].
+
<div><ul>
 +
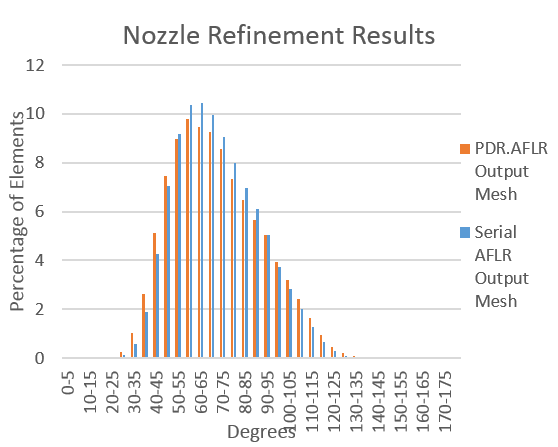
<li style="display: inline-block;"> [[File: nozzle_AFLR.png|thumb|none|350px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: nozzle_stability_1.png|thumb|none|450px|'''(b)''']] </li>
 +
</ul></div>
 +
:(a) shows the nozzle geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
−
= Summary =
+
<div><ul>
 +
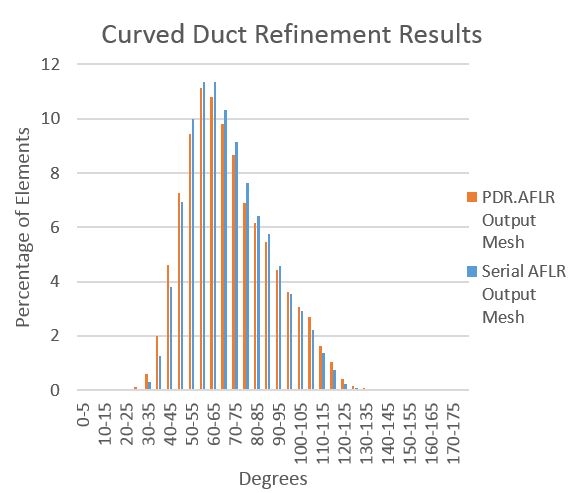
<li style="display: inline-block;"> [[File: curved_duct.png|thumb|none|400px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: curved_duct_stability_1.png|thumb|none|450px|'''(b)''']] </li>
 +
</ul></div>
 +
:(a) shows the curved duct geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
−
= Reproducibility =
+
<div><ul>
 +
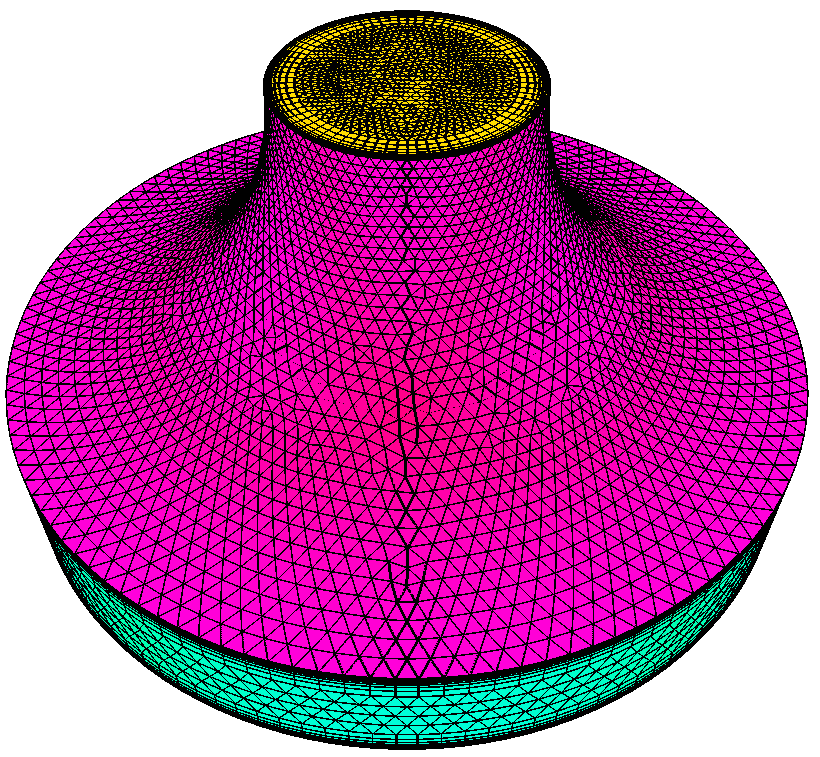
<li style="display: inline-block;"> [[File: radial_nozzle.png|thumb|none|450px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: radial_nozzle_stability_1.png|thumb|none|450px|'''(b)''']] </li>
 +
</ul></div>
 +
:(a) shows the radial nozzle geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
−
= Stability =
+
<div><ul>
 +
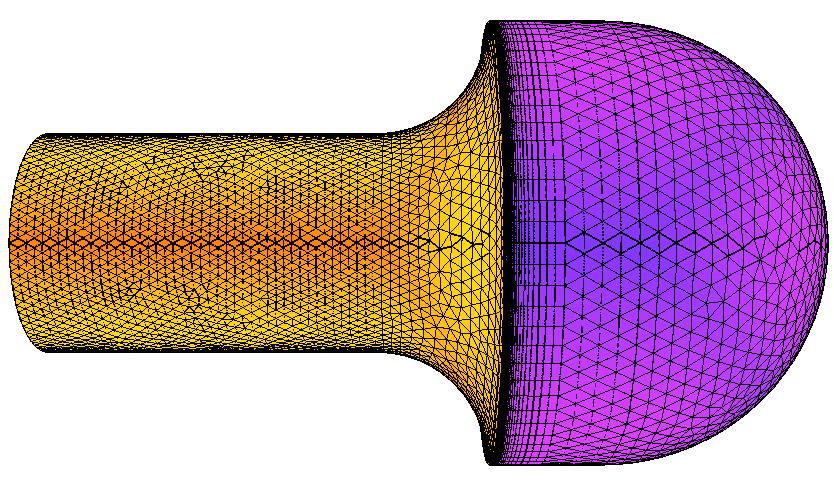
<li style="display: inline-block;"> [[File: horn_bulb.png|thumb|none|500px|'''(a)''']] </li>
 +
<li style="display: inline-block;"> [[File: horn_bulb_stability_1.png|thumb|none|450px|'''(b)''']] </li>
 +
</ul></div>
 +
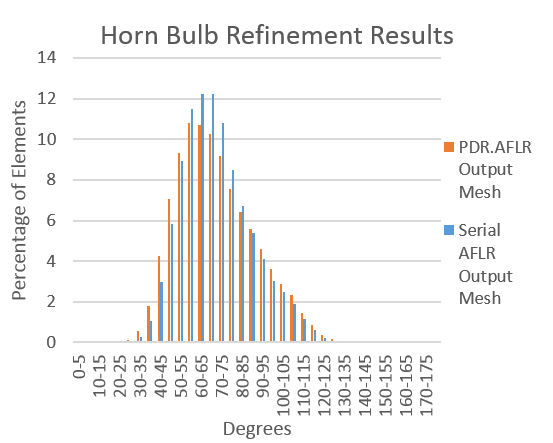
:(a) shows the horn bulb geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.
 +
<br><br><br><br>
  
 
= Scalability =
 
= Scalability =
 +
The parallelization of AFLR is currently a work-in-progress. During runtime, the PDR.AFLR method will expose data decomposition information (number of subdomains waiting to be refined) to our underlying run-time system, PREMA 2.0. In turn, PREMA 2.0 will facilitate work-load balancing and guide the program’s execution towards the most efficient utilization of hardware resources. PREMA 2.0 is a parallel runtime system that supports one-sided communication, global address space and load balancing for adaptive and irregular applications. This runtime system serves as an underlying layer that alleviates the burden of monitoring data and computations in parallel, an ideal candidate to support the execution of PDR.AFLR.

Latest revision as of 12:51, 29 March 2018

Introduction

For the last 30 years, legacy Finite Element (FE) mesh generation methods and software were typically developed with a focus on high performance for single core architectures and without any thought towards scalability for a large number of cores. These codes are still used for production in several industries, including NASA. However, NASA’s Computational Fluid Dynamics (CFD) 2030 Vision will require those highly functional codes to run on large-scale parallel architectures. Highly optimized sequential versions of existing state-of-the-art mesh generation codes, in addition to geometric and numerical challenges imposed by the nature of mesh generation complexity, makes their parallelization a highly challenging problem. In this project, we focus on one of the top, industrial strength mesh generators, called Advancing Front Local Reconnection (AFLR), which is used by NASA, the DoD, and DoE, as well as a number of aerospace industry top research groups. AFLR has not been fully parallelized to properly utilize large-scale supercomputing hardware.

Overview

Modifications were made to AFLR to enable its execution within the Parallel Data Refinement (PDR, a generalized version of Parallel Delaunay Refinement meant to be capable of utilizing any mesh generator, i.e. code re-use) method and software framework (specifically the non-progressive approach) while maintaining AFLR’s full functionality and providing stability i.e., ensuring that the quality of the mesh generated (from each of the individually refined subdomains) is comparable to that of a mesh generated sequentially (by serial AFLR). The quality is defined in terms of the shape and number of the elements. PDR decomposes a meshing problem by using an octree consisting of numerous leaves, or subdomains, that each hold a part of the mesh. The general idea of PDR is to concurrently refine the octree leaves while maintaining mesh conformity. This methodology is proven to generate a conforming mesh after refining the subdomains generated from an input geometry using data decomposition.

Reproducibility

AFLR meets the reproducibility requirement of PDR, as it maintains weak reproducibility (which can be seen in the below example of refinement for the missile geometry). More examples are shown here.

  • Missile1.png
  • Missile reproducibility test.png

Stability

Preliminary results from the initial implementation of the sequential, data-decomposed AFLR show that PDR’s data decomposition does not hinder the quality of the output as it can be seen from the below quality statistics of meshes in comparison to their quality when generated by the serial AFLR. The bar charts show that while the output meshes of the modified AFLR contain slightly more elements of lower quality (percentage of elements towards both ends of the charts), it maintains its stability with a close number of high quality elements to that of the serial AFLR. This implementation is limited to the refinement of manifold, genus zero geometries and will be extended to more complex geometries to satisfy the robustness requirement of PDR in the final version of PDR.AFLR. It is also unable to refine meshes with transparent/embedded surfaces. This will also be addressed in the final version of PDR.AFLR. For simplicity, any transparent/embedded surfaces were removed from certain geometries while testing the stability of the data-decomposed AFLR. This is specified for specific geometries below.

  • (a)
  • (b)
  • (c)
The Fan and Turbine Disk surfaces were removed from the nacelle engine geometry. (a) and (b) show different viewpoints of the geometry. (c) compares the dihedral angle distributions of the output meshes between serial AFLR and PDR.AFLR.





  • (a)
  • (b)
  • (c)
The Plume and NearField embedded surfaces were removed from the missile1 geometry. (a) and (b) show different viewpoints of the geometry. (c) compares the dihedral angle distributions of the output meshes between serial AFLR and PDR.AFLR.





  • (a)
  • (b)
The Plume and NearField embedded surfaces were removed from the missile2 geometry.(a) shows the modified missile2 geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the defroster geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the rocket geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the dome geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the nozzle geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the curved duct geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the radial nozzle geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





  • (a)
  • (b)
(a) shows the horn bulb geometry. (b) shows the dihedral angle distributions of the output meshes compared between the serial AFLR code and PDR.AFLR.





Scalability

The parallelization of AFLR is currently a work-in-progress. During runtime, the PDR.AFLR method will expose data decomposition information (number of subdomains waiting to be refined) to our underlying run-time system, PREMA 2.0. In turn, PREMA 2.0 will facilitate work-load balancing and guide the program’s execution towards the most efficient utilization of hardware resources. PREMA 2.0 is a parallel runtime system that supports one-sided communication, global address space and load balancing for adaptive and irregular applications. This runtime system serves as an underlying layer that alleviates the burden of monitoring data and computations in parallel, an ideal candidate to support the execution of PDR.AFLR.

Retrieved from "https://crtc.cs.odu.edu/index.php?title=PDR.AFLR&oldid=1017"